もういちどだけ内積・外積
この記事の前半では,ベクトルの掛け算である内積と外積を,もう一度じっくり考え直してみます.得になるような話は何も出てきませんので,『もうよく分かってるよ』という人は読まなくてもいいでしょう.内積や外積の計算をしていて,特に何も問題を感じない,という人も読まなくていいでしょう.『一応,計算方法は知ってるけど,なんだか意味がよく分からなくて,気持ちワルイ!』という人,どうぞ読んで見てください.高校生でも読める解説を目指しましたが,とことん理解したいという頑固な人を読者として想定していますので,少し高度な内容も含みます.発展的な内容に関しては,それに関連する分野に触れました.今後の勉強の指針になればと思います.
最後のセクションでは,テンソルの概念に少し触れます.
ベクトルの掛け算
まず二つのベクトル  ,
, 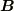 を次のように定義します.この記事で出てくるベクトルは全て
を次のように定義します.この記事で出てくるベクトルは全て 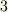 次元とします.太字の
次元とします.太字の  というのは基底ベクトルで,細字の
というのは基底ベクトルで,細字の 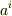 などが成分(スカラー)です.
などが成分(スカラー)です.
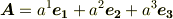
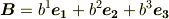
私達は既に,ベクトルには内積と外積という掛け算の仕方があることを知っています.でも,どちらも何だか,普通の数の掛け算の仕方とは,様子が違いました.特に外積というのは,変チクリンな掛け算です.
とりあえず,ベクトル  ,
, 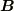 を,"普通に"掛け合わせてみましょう.つまり次式のように,普通に分配則を使って,一つずつ掛け算するのです.ただし,私達はベクトルとベクトルの掛け算がどのような掛け算になるかを決めていませんから,とりあえず,ここでは仮に
を,"普通に"掛け合わせてみましょう.つまり次式のように,普通に分配則を使って,一つずつ掛け算するのです.ただし,私達はベクトルとベクトルの掛け算がどのような掛け算になるかを決めていませんから,とりあえず,ここでは仮に 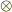 という記号を使っておきます.(掛け算の記号としてお馴染みの
という記号を使っておきます.(掛け算の記号としてお馴染みの  や
や  を使ってしまうと内積や外積の意味になってしまうからです.)
を使ってしまうと内積や外積の意味になってしまうからです.)
Important
係数は実数ですので普通に掛け算します.ベクトルとベクトルの掛け算は,どうやるのか分からないので,とりあえず 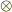 と置いておきます.
と置いておきます.

ここまでは普通の掛け算と同じで,分配則を使って括弧を展開しました. 何もベクトルならではのことをしていません .しかし,私達はまだ  という記号で表される計算が何なのか知りません.次のセクション以下で,この
という記号で表される計算が何なのか知りません.次のセクション以下で,この  にもう少し使い易い算法を与えることを考えましょう.
にもう少し使い易い算法を与えることを考えましょう.
内積
基底の積 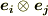 に関して,次のようなルールを決めることにします.
に関して,次のようなルールを決めることにします.
- もし
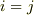 ならば,
ならば, 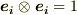 とする.
とする. - もし
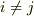 ならば,
ならば, 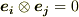 とする.
とする.
すると式 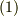 は次のようになります.
は次のようになります.

このルール 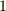 〜
〜  を導入する場合は,特に
を導入する場合は,特に 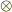 の代わりに
の代わりに  と書くことにしましょう.
と書くことにしましょう.

これはご存知の通り,内積に他なりません.内積とは『二つのベクトルがどれくらい似ているか』を示す量でしたが( 内積空間 参照),上のルールは確かに似ているベクトルだけを選ぶという働きをしています.
外積
今度は,次のようなルールを導入してみましょう.
- もし
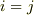 ならば,
ならば, 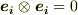 とする.
とする. - もし
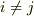 ならば,
ならば, 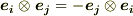 とする.
とする.
すると式 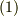 は次のようになります.
は次のようになります.
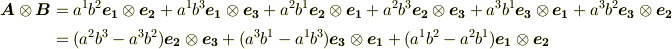
これは,なんだか外積のような形になっていますね.もう一つ,次のようなルールを導入してみましょう.
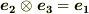 ,
, 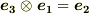 ,
, 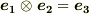 とする.
とする.
すると,この結果は次のようなベクトルになります.これは既に外積としてよく知っている形ですから,左辺は 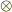 の代わりに
の代わりに  と書くことにしましょう.
と書くことにしましょう.
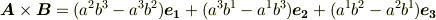
外積は,ベクトルの向きが同じなら零になってしまい,直交するときに大きさが最大となります.これは『二つのベクトルがどれくらい違っているか』を示す指標になると考えられます.
| [*] | 『ルールを入れる』と気安く言いましたが,これが具体的にはどういうことなのか気になった人がいると思います.これについては,テンソル代数を勉強したあと, 外積代数 カテゴリーへ進んでみて下さい.そこで, 代数学 で勉強した類別という概念を使って,ルールを導入する方法を勉強します. |
| [†] | 内積のルール1と外積のルール2を組み合わせたルールを,クリフォード代数と呼びます.数学にも,色々な分野があるものですねぇ. |
考察
内積
式  で行った掛け算にはちゃんと名前がついていて,実はテンソル積と言います.テンソル積に対し,特別にルールを課すと,内積と外積という掛け算を作ることを見ました.基底の積が
で行った掛け算にはちゃんと名前がついていて,実はテンソル積と言います.テンソル積に対し,特別にルールを課すと,内積と外積という掛け算を作ることを見ました.基底の積が  のように同じ基底の積になっているものだけを内積と呼び,同様に
のように同じ基底の積になっているものだけを内積と呼び,同様に  のように異なる基底の積になっているものを外積と呼びましたが,テンソル積の成分を次のように行列で書くと,テンソル積成分のうちどこが内積部分と外積部分に相当するのかがよく分かります.
のように異なる基底の積になっているものを外積と呼びましたが,テンソル積の成分を次のように行列で書くと,テンソル積成分のうちどこが内積部分と外積部分に相当するのかがよく分かります.
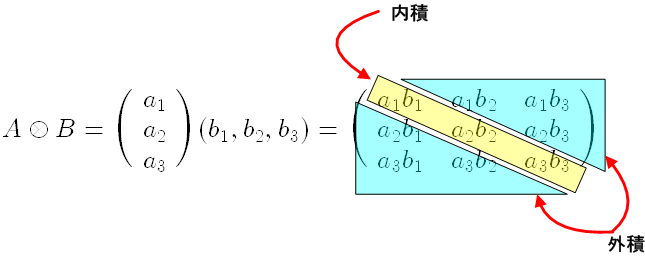
線形代数で出てきたことですが,内積は,このテンソル成分の表現行列の対角和(トレース)になっています.行列のトレースは,直交行列を掛けても不変の量だということでした.直交行列を掛けるというのは,長さを変えないような座標変換を行う操作と同じことです.これを 直交変換 と呼びます.
内積は 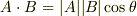 と書くことが出来ましたから,ベクトルの長さと,間の角だけで決まる量で,二つのベクトルの幾何学的な関係だと言えます.長さを変えない座標変換では,見え方が変わるだけで,長さや角度の測り方はは変わりませんから,内積は,長さを変えない座標変換に対して不変な量(スカラー)です.このことは内積の図形的意味を考えれば直観的に明らかですし, 計量テンソル と 直交座標系 では双対基底の性質から確認しましたが,線形代数と一次変換を少し勉強したことがあれば,行列の対角和という見方からも納得がいくでしょう.
と書くことが出来ましたから,ベクトルの長さと,間の角だけで決まる量で,二つのベクトルの幾何学的な関係だと言えます.長さを変えない座標変換では,見え方が変わるだけで,長さや角度の測り方はは変わりませんから,内積は,長さを変えない座標変換に対して不変な量(スカラー)です.このことは内積の図形的意味を考えれば直観的に明らかですし, 計量テンソル と 直交座標系 では双対基底の性質から確認しましたが,線形代数と一次変換を少し勉強したことがあれば,行列の対角和という見方からも納得がいくでしょう.
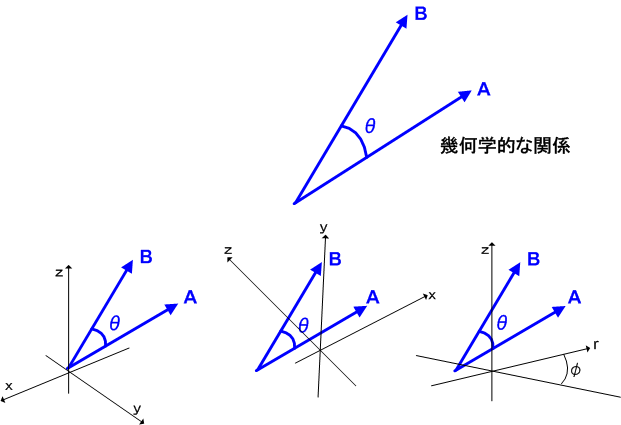
| [‡] | 拡大・縮小のような長さを変える変換では内積の値も変わります.しかし,そもそもベクトルの長さは内積によって定義されるものなので( 内積空間 参照),長さを変える変換とは取りも直さず内積を変える変換だとも言えるわけです.内積を変える変換で内積が変わるのは当然です.上の説明では,直観的理解に訴えるため,『幾何学的関係は見る人によらない⇒内積は不変』というような説明をしましたが,厳密に言えば内積によって幾何学的関係が決まるのであり,内積が定義できなければ私達が使いたいような意味での距離とか角度という概念も入ってきません. |
外積
外積の向きは,基底ベクトルを右手系と左手系のどちらと定めるかによって変わってきます.いわば向きは任意に決めたものだと言えます( 軸性ベクトルと極性ベクトル 参照).
また,私達の知っているような外積は,三次元と七次元のベクトルでしか定義できないことが知られています( 七次元のベクトル 参照).これは,外積のところで導入したルール 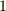 〜
〜 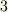 がうまく成り立つのは,三次元か七次元しかないということです.外積の計算を行うには,なかなか条件が厳しいようですね.外積のルール
がうまく成り立つのは,三次元か七次元しかないということです.外積の計算を行うには,なかなか条件が厳しいようですね.外積のルール 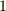 と
と  を持った算法の構造を,外積代数と呼びます.外積代数では,外積の計算を一般の次元でも使えるように少し拡張したウェッジという乗法を考えます.これはなかなか魅力的な世界ですので,そのうち改めて紹介したいと思います.
を持った算法の構造を,外積代数と呼びます.外積代数では,外積の計算を一般の次元でも使えるように少し拡張したウェッジという乗法を考えます.これはなかなか魅力的な世界ですので,そのうち改めて紹介したいと思います.
テンソル
私達は,最初にそのままベクトルを掛け合わせ,そこに独特のルールを課することで内積と外積を分離しましたが,何も分離しないで,そのままテンソル積 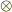 の形で考えることもできます.このようにして出てきた量は,テンソルと呼ばれます.もう一度,式
の形で考えることもできます.このようにして出てきた量は,テンソルと呼ばれます.もう一度,式 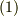 を眺めてみましょう.
を眺めてみましょう.
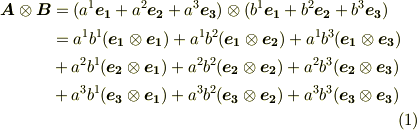
基底として, 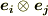 の形のものが大量に出てきましたが,これらはこれ以上変形したり簡単には出来ない独立なものとして,そのままにしておきます.つまり,これらを
の形のものが大量に出てきましたが,これらはこれ以上変形したり簡単には出来ない独立なものとして,そのままにしておきます.つまり,これらを 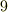 種類の独立な基底と考えるわけです.
種類の独立な基底と考えるわけです.
私達は,ベクトル 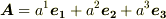 を,基底
を,基底 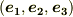 に対する係数だけをまとめて
に対する係数だけをまとめて 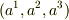 のように表現しましたが,同じように式
のように表現しましたが,同じように式 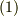 の右辺も,各基底
の右辺も,各基底 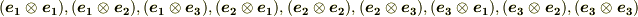 に対する成分だけを次のようにまとめて書くことができます.
に対する成分だけを次のようにまとめて書くことができます.
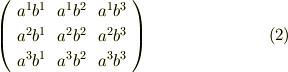
この行列は既に,さきほど内積のセクションで少し紹介したものです.いま,二つのベクトルのテンソル積を考えて出てきたテンソルですから,これを二階のテンソルといいます.二階のテンソルの成分は,上のように 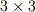 行列で書かれることが多いです.三つのベクトルのテンソル積を取れば三階のテンソルになります.三階のテンソルの基底は
行列で書かれることが多いです.三つのベクトルのテンソル積を取れば三階のテンソルになります.三階のテンソルの基底は 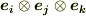 の形で,成分は
の形で,成分は 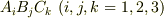 のようになります.(
のようになります.( 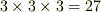 成分ですね.)
成分ですね.)
| [§] | たまに,テンソルのことを行列だと勘違いしている人に遭遇します.この勘違いは恐らく,物理学や工学に出てくるテンソルの多くが二階のテンソルで,式  の行列形でいきなり教科書に紹介されることに原因していると思われます.式 の行列形でいきなり教科書に紹介されることに原因していると思われます.式  のように基底に着目し,ベクトルを拡張したものがテンソルだということが分かっていれば,テンソルを単なる行列だと勘違いすることは無いでしょうし,三階以上のテンソル成分を行列で表わそうと思ったら少し工夫が必要だということも察せられるでしょう. のように基底に着目し,ベクトルを拡張したものがテンソルだということが分かっていれば,テンソルを単なる行列だと勘違いすることは無いでしょうし,三階以上のテンソル成分を行列で表わそうと思ったら少し工夫が必要だということも察せられるでしょう. |
いま,ベクトルをそのまま掛ける演算として,テンソル積とテンソルの概念を紹介しました.上で見たように,テンソルの基底を考え,その成分としてテンソルを定義する見方は,ベクトルの自然な拡張として理解しやすいアプローチだと思います.テンソルには他に,座標変換の際に満たすべ関係式や,多重線形性と呼ばれる線形性を拡張した性質など,テンソルの特徴ともいうべき大事な性質があり,それらをテンソルの定義とする立場もあります.
このあと テンソルの概念 では,テンソル成分が座標変換の際に満たすべき関係式を使ってテンソルを定義します.テンソルは結構奥の深い分野ですから,それだけで色々楽しめると思います.
| [¶] | ベクトルの集合は ベクトル空間 と呼ばれる代数構造を持ちますが,ベクトルの元同士に適切な乗法を定義したベクトル空間を代数と呼びます.代数と言うと,代数学の意味もありますから紛らわしいですが,数学者は乗法の定義されたベクトル空間を代数と呼んでしまっても混乱しないようです.テンソル積によってベクトル空間から生成される代数は テンソル代数 と呼ばれます. |