多重線形性とテンソル空間
ここまで勉強したことを少しおさらいしておきましょう.ベクトル空間 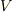 とその双対空間
とその双対空間 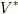 という考え方がベクトル代数に出てきましたが,そこで考えた線形性を二変数関数にまで拡張し,双線形性という性質を考えることで,新たにベクトル空間
という考え方がベクトル代数に出てきましたが,そこで考えた線形性を二変数関数にまで拡張し,双線形性という性質を考えることで,新たにベクトル空間 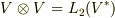 という概念に到達しました.そして,
という概念に到達しました.そして, 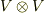 の元は,私達が今まで考えてきた二階のテンソルであることを確認しました.
の元は,私達が今まで考えてきた二階のテンソルであることを確認しました.
同様にして,多変数関数に対して多重線形性という性質を考えることで,さらに高次のベクトル空間 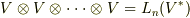 を考えることが出来ます.このようにして生成したベクトル空間を,一般には テンソル空間 と呼び,記号
を考えることが出来ます.このようにして生成したベクトル空間を,一般には テンソル空間 と呼び,記号 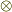 をテンソル積と呼ぶのでした.
をテンソル積と呼ぶのでした.
ここまでのところをよく整理・復習してから先に進んで下さい.
多重線形性
多重線形性という性質は,線形性を多変数関数にまで拡張したものです.多変数関数 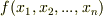 に対し,
に対し, 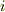 番目の変数
番目の変数 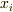 を
を 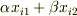 と置くとき,次の性質を満たす関数を 多重線形関数 と呼びます.
と置くとき,次の性質を満たす関数を 多重線形関数 と呼びます.
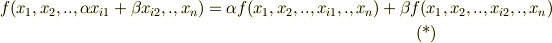
つまり,  個の変数に対し,各々個別に線形性が成り立つ関数だということです.ここでは証明は省略しますが,
個の変数に対し,各々個別に線形性が成り立つ関数だということです.ここでは証明は省略しますが, 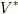 上の多重線形関数の集合はテンソル空間と呼ばれるベクトル空間になり,
上の多重線形関数の集合はテンソル空間と呼ばれるベクトル空間になり, 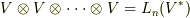 と書けます.(余力のある人は証明してみて下さい. 双線形関数 で示した証明を一般の
と書けます.(余力のある人は証明してみて下さい. 双線形関数 で示した証明を一般の  変数関数にまで拡張するだけです.)
変数関数にまで拡張するだけです.)
テンソル空間の基底は 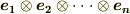 の形で,成分は
の形で,成分は 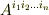 の形に表現できます.また,ある基底の組に対して表現は一意的です.これらの証明は テンソルとベクトル空間 で示した証明と基本的には同じですので,ここでは省略します.
の形に表現できます.また,ある基底の組に対して表現は一意的です.これらの証明は テンソルとベクトル空間 で示した証明と基本的には同じですので,ここでは省略します.
テンソルの直積
このセクションでは,テンソル空間の元同士の積がどうなるかを考えます.代数的な議論が苦手で,結果だけを了承したい読者の方は,この記事を飛ばして テンソルの加法と乗法 に進んでも大丈夫でしょう.
私達は, テンソルとベクトル空間 の記事で, 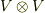 の写像(関数)を次のように定義しました.
の写像(関数)を次のように定義しました.
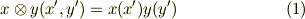
左辺を 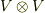 空間のひとつの元と見ても良いですが,
空間のひとつの元と見ても良いですが, 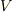 の二つの元の間にテンソル積という新しい乗法を導入したと見ても良いでしょう.これから考えるのはまさに,テンソル空間の元同士のテンソル積です.(ベクトル空間
の二つの元の間にテンソル積という新しい乗法を導入したと見ても良いでしょう.これから考えるのはまさに,テンソル空間の元同士のテンソル積です.(ベクトル空間 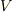 のテンソル積からテンソル空間
のテンソル積からテンソル空間 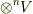 を考えましたが,まだ
を考えましたが,まだ 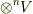 の元同士の演算は考えていませんでした.)
の元同士の演算は考えていませんでした.)
いま,式 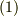 を拡張し,
を拡張し,  の元
の元 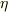 と
と 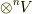 の元
の元 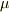 の元のテンソル積
の元のテンソル積  の,
の, 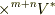 (
( 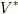 の直積集合)への作用を次式のように定義します.
の直積集合)への作用を次式のように定義します.
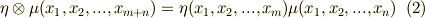
式 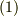 が式
が式 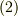 の特別な場合であることが分かると思います.また,式
の特別な場合であることが分かると思います.また,式 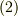 を右辺から左辺へと読むと,『
を右辺から左辺へと読むと,『  の元
の元 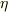 と
と 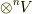 の元
の元 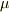 の積が
の積が 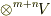 の元
の元  になる』とも読めますので,これはテンソル同士の掛け算を意味していると考えられます.
になる』とも読めますので,これはテンソル同士の掛け算を意味していると考えられます.
一般に,積というのは何らかの作用を意味します.( 群の公理 参照.)逆演算(割り算)がきちんと定義できる積もあれば,零を掛けたり定数に微分演算子を作用させるときのように,元に戻れなくなってしまう積もあります.また,行列の積のように交換則がなりたたないものや,十六元数の積( 七次元の外積 参照)のように結合則までなりたたないような積まで,その性質や扱い易いさには様々な段階があります.
| [*] | 代数学的な視点では,結合則・交換則・逆演算の可能性など,演算の構造がとても大事です.それによって,その演算が定義された集合が,集合としてどのような性質を持つものであるかが調べられるからです.私達は今,かなり代数的な視点でテンソルの積を考えています.あまり代数学に馴れていない人は,分配則とか結合則と言われてもあまり面白くないかも知れません.この際,代数学もやってしまおうという人は こちら へどうぞ. |
式 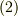 で与えられる積は,次のような性質を満たすことが示せます.
で与えられる積は,次のような性質を満たすことが示せます.
【結合則】

【分配則】
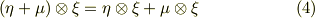
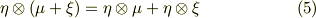
しかし, 一般に交換則はなりたちません .テンソルの積は非可換だということです.

このことは,例えば 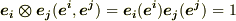 と,
と, 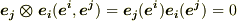 が異なることを考えれば良いでしょう.
が異なることを考えれば良いでしょう.
積の成分
ここまでの議論を使って,テンソルの積におけるテンソル成分の関係を求めておきます.  の元
の元 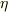 と
と 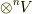 の元
の元 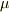 は,それぞれ基底
は,それぞれ基底 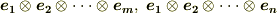 と適当な係数を使って次のように表現できるでしょう.
と適当な係数を使って次のように表現できるでしょう.

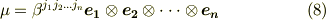
式 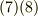 の両辺のテンソル積を取ると次式を得ます.
の両辺のテンソル積を取ると次式を得ます.
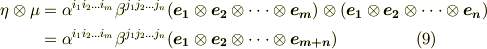
一方, 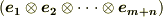 を基底とするテンソルは,
を基底とするテンソルは, 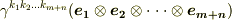 のように表現できるはずです.式
のように表現できるはずです.式 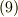 と見比べ,成分に関して次式を得ます.
と見比べ,成分に関して次式を得ます.
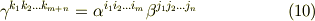
これは,テンソル成分の テンソル積 (もしくは 外部積 )と呼ばれている演算で, 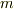 階のテンソル成分と
階のテンソル成分と  階のテンソル成分の積は
階のテンソル成分の積は 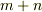 階のテンソル成分になることがわかりました.テンソルの加法と乗法_ でもう一度取り上げます.
階のテンソル成分になることがわかりました.テンソルの加法と乗法_ でもう一度取り上げます.