方向微分
スカラー場 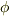 に対し,空間のある点(
に対し,空間のある点( 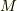 とします )において,勾配ベクトルと呼ばれる量
とします )において,勾配ベクトルと呼ばれる量 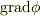 を定義しました.意味がよく分からない人は スカラー場と勾配 をもう一度復習してください.勾配ベクトルはベクトルの形で表わされていますが,特定の方向への勾配ならば,その方向へ勾配ベクトルを射影することで,スカラーで表わすことができます.いま,点
を定義しました.意味がよく分からない人は スカラー場と勾配 をもう一度復習してください.勾配ベクトルはベクトルの形で表わされていますが,特定の方向への勾配ならば,その方向へ勾配ベクトルを射影することで,スカラーで表わすことができます.いま,点 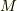 において,ある方向(
において,ある方向( 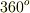 どの向きでも良い)を決めるとき,その方向に沿った勾配を表わす方法を考えてみます.
どの向きでも良い)を決めるとき,その方向に沿った勾配を表わす方法を考えてみます. 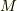 から少し離れた点を
から少し離れた点を 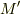 とし,
とし, 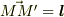 と置きます.この方向を考えます.
と置きます.この方向を考えます.
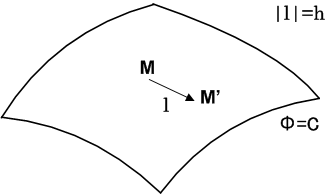
このとき,スカラー場 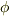 の点
の点 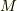 における
における 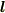 方向の勾配は,微分の定義より次のように与えられるでしょう.二点間の距離を
方向の勾配は,微分の定義より次のように与えられるでしょう.二点間の距離を 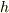 とします.(
とします.( 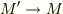 のとき
のとき 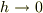 となります.)
となります.)
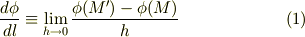
このように,スカラー場の一点における,特定の方向に関する変化率を 方向微分 と呼び, 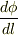 を φのl方向の方向微係数 と呼びます.式
を φのl方向の方向微係数 と呼びます.式 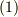 に出てくる
に出てくる 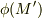 は,
は, 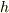 を微小な量だとすると,偏微分を使って次のように表わせるでしょう.
を微小な量だとすると,偏微分を使って次のように表わせるでしょう.
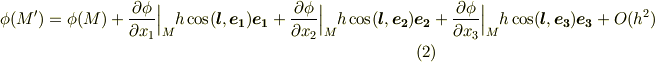
式中, 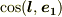 などの括弧中は『
などの括弧中は『 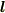 と
と 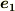 のなす角』の意味とします.また
のなす角』の意味とします.また 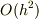 は『
は『 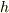 の二次以上の項』という意味とします.式
の二次以上の項』という意味とします.式 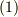 に式
に式 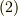 を代入して,次式のように式を展開できます.
を代入して,次式のように式を展開できます.
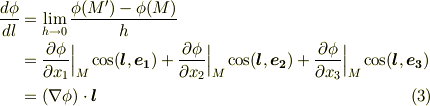
方向微係数はずいぶん簡単な式で表わすことが出来ました.ここで 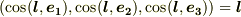 ですが,これは内積の公式
ですが,これは内積の公式 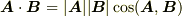 を使えばすぐに示せますので,引っかかる人は自分で確認してみて下さい.
を使えばすぐに示せますので,引っかかる人は自分で確認してみて下さい.
theorem
スカラー場 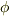 の点
の点 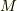 における
における 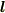 方向への方向微係数は
方向への方向微係数は 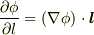 で与えられます.
で与えられます.
内積の意味を思い出し,『ベクトル 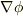 の,
の, 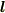 への射影』と考えれば,この結果はむしろ当然で,最初からいきなり書き下しても良さそうなものですが,少し丁寧に導いてみました.
への射影』と考えれば,この結果はむしろ当然で,最初からいきなり書き下しても良さそうなものですが,少し丁寧に導いてみました.
| [*] | 勾配ベクトルは座標基底 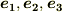 の方向の成分だけで表わされていますが,それによって の方向の成分だけで表わされていますが,それによって 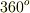 全方位の方向微分を表わすことに問題は無いのでしょうか? (例えば,基底と違う方向にびっくりするぐらい急な傾きを持っていたりとか, 全方位の方向微分を表わすことに問題は無いのでしょうか? (例えば,基底と違う方向にびっくりするぐらい急な傾きを持っていたりとか, 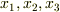 の各軸方向にだけ勾配があって,他の方向には何の変化も無いとか,そんな特殊な場合でも方向微分は使えるのでしょうか?)このような疑問を持つ人がいるかも知れません.いま方向微係数を定義できるための条件として, の各軸方向にだけ勾配があって,他の方向には何の変化も無いとか,そんな特殊な場合でも方向微分は使えるのでしょうか?)このような疑問を持つ人がいるかも知れません.いま方向微係数を定義できるための条件として, 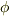 は は 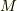 の近傍で十分に滑らかで連続だと仮定しています.本当は,最初から厳密にこういうことを言い並べて議論を進めれば良いのですが,それでは退屈な数学の教科書のようになってしまうので省きました.(この註は気になる人だけ読んでくれればいいんですよ.)スカラー場 の近傍で十分に滑らかで連続だと仮定しています.本当は,最初から厳密にこういうことを言い並べて議論を進めれば良いのですが,それでは退屈な数学の教科書のようになってしまうので省きました.(この註は気になる人だけ読んでくれればいいんですよ.)スカラー場 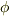 が十分に滑らかで連続であるというのは, が十分に滑らかで連続であるというのは, 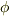 がビックリするほど急に変化したりはしないという仮定です.今,私達が考えているのは三次元ユークリッド空間ですが,この仮定は,どこでも局所的に三次元の座標系を描けるということと同じです.ということは,ベクトルは がビックリするほど急に変化したりはしないという仮定です.今,私達が考えているのは三次元ユークリッド空間ですが,この仮定は,どこでも局所的に三次元の座標系を描けるということと同じです.ということは,ベクトルは 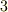 つの成分に分解できる,という仮定でもあります.解析的には,式 つの成分に分解できる,という仮定でもあります.解析的には,式 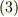 で で 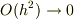 となったことがこの仮定に対応しています.全方位の変化率を, となったことがこの仮定に対応しています.全方位の変化率を, 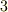 成分のベクトルで表わせるのは,少し不思議な感じがしますが,これが線形ということであり,一次近似ということなんです.(微分的に見るということは,変化を線形化してしまうということです.線形って,便利ですね!) 成分のベクトルで表わせるのは,少し不思議な感じがしますが,これが線形ということであり,一次近似ということなんです.(微分的に見るということは,変化を線形化してしまうということです.線形って,便利ですね!) |