よくある間違い
公式集を見ると,ベクトル演算子 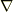 に関係した公式がたくさん載っていますが,全部を覚えるのは大変です.それらを自分で導かなければならなくなったとき,ありがちな間違いがあります.例えば,次の公式を導きたいとします.(右辺が分からないとします.)
に関係した公式がたくさん載っていますが,全部を覚えるのは大変です.それらを自分で導かなければならなくなったとき,ありがちな間違いがあります.例えば,次の公式を導きたいとします.(右辺が分からないとします.)
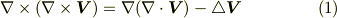
これを導くのに何か使える公式なかったかなぁ・・・と教科書をパラパラめくって,次の公式を見つけたとしましょう.
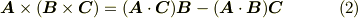
『やや,この左辺の形は使えそうだぞ!じゃあこの公式で, 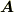 と
と 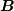 を
を 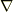 と置いて,
と置いて, 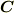 を
を 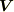 と置けばいいか!!』と喜び勇んで代入してみると・・・.
と置けばいいか!!』と喜び勇んで代入してみると・・・.
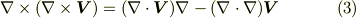
何だか式 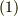 とは違った式が出てきてしまいました.
とは違った式が出てきてしまいました. 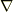 だって一種のベクトルなのに,何がいけなかったんでしょうか?式
だって一種のベクトルなのに,何がいけなかったんでしょうか?式 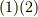 は正しい公式で,式
は正しい公式で,式 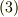 は間違いです.ここまで読んで,なぜ式
は間違いです.ここまで読んで,なぜ式 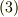 が間違いなのかがよく分からない人は,先を読む前にじっくり理由を考えて見てください.
が間違いなのかがよく分からない人は,先を読む前にじっくり理由を考えて見てください.
なぜ▽をベクトルの公式に代入しては駄目か
なぜ, 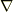 をそのままベクトルの公式に代入してはいけないかを考えてみましょう.確かに
をそのままベクトルの公式に代入してはいけないかを考えてみましょう.確かに 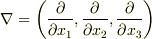 はベクトルですが,『右から掛かってきたものを微分する』という特別な作用を持っています.
はベクトルですが,『右から掛かってきたものを微分する』という特別な作用を持っています.
つまり,普通のベクトルならば 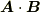 と
と 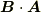 は同じですが,
は同じですが, 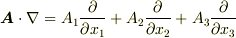 は,右から何かが掛かってくればたちまち微分してしまう微分演算子であり,一方,
は,右から何かが掛かってくればたちまち微分してしまう微分演算子であり,一方, 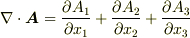 は微分演算子ではなく,
は微分演算子ではなく, 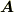 の発散
の発散 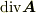 になっています.
になっています.
つまり,内積をとるにせよ外積を取るにせよ, ▽は右から作用させる場合と左から作用させる場合では意味が違う のです.式 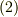 のような,定ベクトルだけの公式は,たいていの場合
のような,定ベクトルだけの公式は,たいていの場合 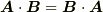 のような関係を用いて式を整理してしまってありますので,途中変形での積の順番が無視されてしまっている場合が多く,そのままでは
のような関係を用いて式を整理してしまってありますので,途中変形での積の順番が無視されてしまっている場合が多く,そのままでは 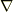 を代入できません.
を代入できません.
Important
ベクトルの公式に,そのまま 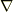 を代入するのはやめましょう.
を代入するのはやめましょう.
ベクトル演算子を含んだ公式を導くには,多少面倒ですが, テンソル記号を使ってベクトル公式を導く が確実です.