双線形関数
ベクトルは,抽象的にはベクトル空間という集合の元だと考えられました( ベクトル空間と線形写像 参照).ベクトル空間の元で本質的に重要なのは 線形性 という性質です.つまり,ベクトル空間の元を 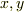 ,適当なスカラーを
,適当なスカラーを 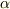 とすると,関係式
とすると,関係式 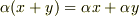 がなりたつということです.
がなりたつということです.
このような抽象的な代数構造は,慣れないと無味乾燥な議論に思えるかも知れませんが,数学的な構造を理解するのには大変に強力です.たとえば,ベクトル空間  上の線形汎関数は,線形関数であって(つまり
上の線形汎関数は,線形関数であって(つまり 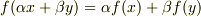 を満たすということ),
を満たすということ),  の双対空間と呼ばれるベクトル空間
の双対空間と呼ばれるベクトル空間 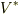 を形成することを見ました.( 双対空間 を参照.)これは大変に面白い結果ですが,抽象的な数学の議論に慣れていないと,ちょっとすぐには思いつかないでしょう.このような代数的な構造が分かると,共変ベクトルと反変ベクトルという二つの体系が織り成す双対の世界がクリアに見えてきます.ここまではベクトル代数の復習です.
を形成することを見ました.( 双対空間 を参照.)これは大変に面白い結果ですが,抽象的な数学の議論に慣れていないと,ちょっとすぐには思いつかないでしょう.このような代数的な構造が分かると,共変ベクトルと反変ベクトルという二つの体系が織り成す双対の世界がクリアに見えてきます.ここまではベクトル代数の復習です.
私達は テンソルの概念 で紹介したように,ベクトルを拡張したテンソルという概念を導入しました.この記事では,テンソルの代数的な構造を考えてみます.抽象的な議論が苦手な人は読まなくても大丈夫ですが,しっかりとテンソルを理解したい人にはぜひ一度ゆっくり考えてみて欲しい内容です.
まず手始めに,二階のテンソルが,どのようにベクトル(一階のテンソル)の拡張になっているのかを考えます.次のセクションはそのための準備として,線形関数の持っていた線形性という性質を,二変数の関数にまで拡張した 双線形性 という概念を紹介するところから始めます.頑張りましょう.
まずは記号
議論に先立って,これから使う記号を導入しておきます.ベクトル空間  の元は,その双対空間
の元は,その双対空間 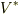 の元から見れば線形汎関数になっていました.つまり,
の元から見れば線形汎関数になっていました.つまり, 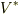 の元を
の元を 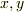 とすると,『
とすると,『  の元は
の元は 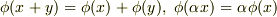 を満たす関数(写像)
を満たす関数(写像) 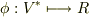 である』ということです.つくづく視点の変換は大事ですね.
である』ということです.つくづく視点の変換は大事ですね.
このことを,次のように記号で書くことにします.
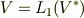
右辺の 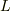 は線形(
は線形( 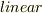 )の意味で,『
)の意味で,『  は
は 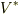 上の線形汎関数の集合だよ』というです.
上の線形汎関数の集合だよ』というです. 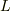 の添字
の添字  の意味は,線形関数が
の意味は,線形関数が 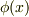 のように一変数関数だという意味です.
のように一変数関数だという意味です.  をわざわざ
をわざわざ 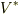 を使って定義するわけですね.また,あとで比較するので,線形関数の性質を復習しておきます.
を使って定義するわけですね.また,あとで比較するので,線形関数の性質を復習しておきます.
【線形関数の性質】
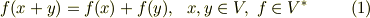
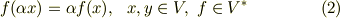
式 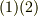 を一つに組み合わせて次のように書いてしまうこともあります.
を一つに組み合わせて次のように書いてしまうこともあります.
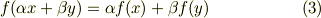
双線形関数
ベクトル代数の分野で考えた線形汎関数は一変数でしたが,ここでは二変数の線形汎関数を考えます.ベクトル空間 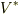 の元
の元 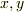 に対し, 二変数の関数
に対し, 二変数の関数 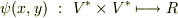 を考えるわけです.(この辺りで議論がしんどく感じる人は,もう一度 ベクトル空間と線形写像 , 双対空間 を復習して下さい.
を考えるわけです.(この辺りで議論がしんどく感じる人は,もう一度 ベクトル空間と線形写像 , 双対空間 を復習して下さい. 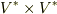 は直積集合で,
は直積集合で, 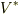 の元を二つセットにした変数
の元を二つセットにした変数 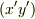 の集合です.)
の集合です.)
ベクトルの双対基底を考えたときは,一変数の線形関数だけを考えていましたが,これから線形性の概念を二変数の関数 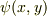 にまで拡張します.二変数の組
にまで拡張します.二変数の組  は
は 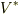 の直積集合
の直積集合 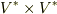 上の元であることに注意しましょう.
上の元であることに注意しましょう.
ベクトル空間 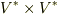 の元に対し,関数
の元に対し,関数  が次の性質を満たすとき,これを
が次の性質を満たすとき,これを 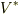 上の 双線形関数 と呼びます.
上の 双線形関数 と呼びます.
【双線形関数の性質】
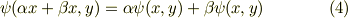
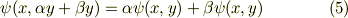
線形関数の性質  とよく見比べてみて下さい.双線形関数は 個々の変数に対して別々に線形性を持っている と言えそうです.これが双線形という名前の由来でもあります.
とよく見比べてみて下さい.双線形関数は 個々の変数に対して別々に線形性を持っている と言えそうです.これが双線形という名前の由来でもあります.
双線形関数のつくるベクトル空間
双線形関数の集合はベクトル空間を形成します! 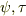 を
を 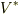 上の双線形関数として,そのことを見てみましょう.
上の双線形関数として,そのことを見てみましょう.
【和 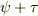 が双線形性を持つこと】
が双線形性を持つこと】
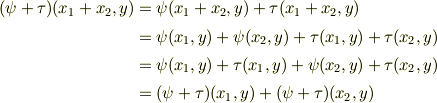
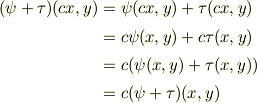
【スカラー積  が双線形性を持つこと】
が双線形性を持つこと】
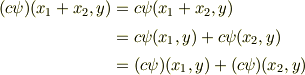
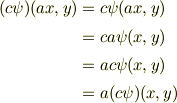
証明では  に関する線形性だけを示しましたが,
に関する線形性だけを示しましたが,  に対しても全く同様になりたちます.これより,
に対しても全く同様になりたちます.これより,  上の双線形関数
上の双線形関数  に対し,和
に対し,和 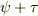 とスカラー倍
とスカラー倍  もやはり双線形関数となり, 双線形関数の全体はベクトル空間を形成する ということが分かりました.このベクトル空間はいわば
もやはり双線形関数となり, 双線形関数の全体はベクトル空間を形成する ということが分かりました.このベクトル空間はいわば 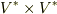 の双対空間ですから,
の双対空間ですから, 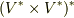 と書いても良いでしょうが,これを特に
と書いても良いでしょうが,これを特に 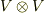 と書くことにします.(
と書くことにします.( 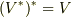 でしたから,
でしたから, 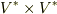 に対する双線形汎関数の集合が
に対する双線形汎関数の集合が  で表現できることは何となく予想できると思いますが,このことは後できっちり示します.)
で表現できることは何となく予想できると思いますが,このことは後できっちり示します.) 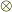 を テンソル積 と呼びます.普通に
を テンソル積 と呼びます.普通に 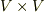 と書くと,
と書くと, 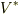 の元を二つ,特に何の決まりも定めずにワンセットにした元の集合のように読めてしまいますので,それと区別し,『
の元を二つ,特に何の決まりも定めずにワンセットにした元の集合のように読めてしまいますので,それと区別し,『 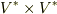 の元に対して, 双線形関数が作るベクトル空間 だよ』ということを明示するための記号だと思えば良いと思います.
の元に対して, 双線形関数が作るベクトル空間 だよ』ということを明示するための記号だと思えば良いと思います.
最初に導入した記号を使えば,次のように書いても良いでしょう.
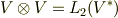
Important
双線形関数の全体は,ベクトル空間( 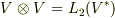 と書く)になります.
と書く)になります.
右辺の添字 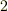 は双線形関数が二変数だからです.ムウゥ!なんだか,徐々に線形関数が一般化されてきたような臭いがしますね.いよいよ次の テンソルとベクトル空間 では,双線形関数の作るベクトル空間の元が,二階のテンソルであることを示します.
は双線形関数が二変数だからです.ムウゥ!なんだか,徐々に線形関数が一般化されてきたような臭いがしますね.いよいよ次の テンソルとベクトル空間 では,双線形関数の作るベクトル空間の元が,二階のテンソルであることを示します.
| [*] | 最初から 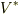 の元に対する双線形汎関数を考えていたのは,最後に の元に対する双線形汎関数を考えていたのは,最後に 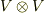 に帰着させたかったからです.ちょっと天下り的でしたが, に帰着させたかったからです.ちょっと天下り的でしたが,  と と 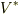 は双対ですから,逆がいい人は は双対ですから,逆がいい人は  と と 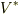 を全部逆に考えても構いません. を全部逆に考えても構いません. |