特別な性質を持つ演算子
量子力学に出てくる演算子の中には,特別な性質を持ったものがいくつかあります. その性質と名称を一緒に覚えましょう.
エルミート演算子とは

つまり,

を満たす演算子  のことを,エルミート演算子といいます.
のことを,エルミート演算子といいます.
エルミート演算子の固有値
エルミート演算子  に対して,
に対して,

という固有値方程式を考えます(固有関数が  で固有値が
で固有値が  ).この式で,
).この式で,  との内積を取ると,
との内積を取ると,

となります.これから,「エルミート演算子の固有値は実数(  )である」ことが分かります.
)である」ことが分かります.
エルミート演算子の異なる固有値に対する固有関数
エルミート演算子  に対して,
に対して,

という固有値方程式を考えます(固有関数が  で固有値が
で固有値が  ).この式で,
).この式で,

を満たす  との内積を取ると,
との内積を取ると,

より,

となります.ここで,  から,
から,

が得られ,「エルミート演算子の異なる固有値に対する固有関数は直交する」ことが分かります.
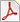


 のことを,演算子
のことを,演算子 
 としたとき,
としたとき,