演算子の性質と交換関係
量子力学にはなくてはならないものの1つが演算子です.その演算子について学びます.演算子とは,関数に作用させて演算を行うもので,量子力学では,さまざまな物理量が演算子で表されます.いきなり演算子と言われても,ぴんとこないと思いますが,例えば,位置を表す  や,運動量を表す
や,運動量を表す  も演算子として扱うことになります.
も演算子として扱うことになります.
演算子の交換関係とは
そこで,演算子  に対して,
に対して,
![[A, B]=AB-BA](./efec139aa86b0245df864b9e485359f8.png)
という量を定義します.これを演算子  の交換関係といいます.
の交換関係といいます.
![[A, B]\neq 0](./d182af7e9d033bd6d85c66ad42e57f21.png)
ならば,「演算子  は交換しない」といい,
は交換しない」といい,
![[A, B]=0](./8f03c9b4f95662b8c250e0520db50475.png)
ならば,「演算子  は交換する」といいます.
は交換する」といいます.
例
冒頭で紹介した,  と
と  について,交換関係を計算してみます.量子力学では,(1次元の場合)
について,交換関係を計算してみます.量子力学では,(1次元の場合)  とします.ここでは,分かりやすいように,この交換関係が後ろの
とします.ここでは,分かりやすいように,この交換関係が後ろの  という関数に作用するとしてみましょう.さらに,
という関数に作用するとしてみましょう.さらに,  や
や  が演算子であることを強調するために,
が演算子であることを強調するために,  と書くことにします.
と書くことにします.
![[\hat{x}, \hat{p}]\phi(x)&=\left[\hat{x}, -i\hbar \frac{\partial}{\partial x}\right]\phi(x)=-i\hbar\left[\hat{x}, \frac{\partial}{\partial x}\right]\phi(x)\\&=-i\hbar\left(\hat{x}\frac{\partial}{\partial x}-\frac{\partial}{\partial x}\hat{x}\right)\phi(x)=-i\hbar\left(x\frac{\partial \phi(x)}{\partial x}-\phi(x)-x\frac{\partial \phi(x)}{\partial x}\right)=i\hbar\phi(x)](./27fe34449d897c5432871a149a1e043f.png)
となって,
![[\hat{x}, \hat{p}]\phi(x)=i\hbar\phi(x)](./af9b22d527f0d76e12f2dc5161ce6376.png)
つまり,
![[\hat{x}, \hat{p}]=i\hbar](./7c05df4e9a37155b9d967632a9fd301f.png)
と求まります.  をすぐに
をすぐに  としてしまいがちですが,
としてしまいがちですが,  は後ろの
は後ろの  にもかかっていますので,上記のような計算結果となります.
にもかかっていますので,上記のような計算結果となります.
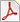

 がある時,
がある時,

 があるとき,交換関係について,以下の式が成り立つことを示しなさい.
があるとき,交換関係について,以下の式が成り立つことを示しなさい.![[A, BC]=[A, B]C+B[A, C]](./b3752423af200a73b604a58e09082588.png)
![[AB, C]=A[B, C]+[A, C]B](./825572c4a5020c218ead6c2bed20e6a5.png)