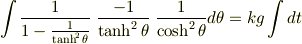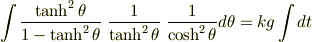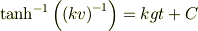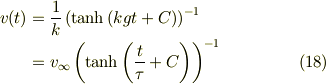抵抗力のある落下運動 2
抵抗力のある落下運動 では抵抗力が速度に比例する運動を考えました.
そこでは終端速度が 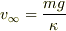 となることを学びました.
となることを学びました.
ここでは抵抗力が速度の二乗に比例する場合(慣性抵抗と呼ばれています)にどのような運動になるかを見ていきます.
運動方程式
落下運動に限らず,重力下で慣性抵抗を受けながら運動する物体の運動方程式は,次のようになります.
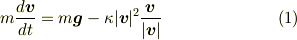
この記事では話を簡単にするために,鉛直方向の運動のみを扱うことにします. つまり落下運動または鉛直投げ上げということになります. このとき (1) は,
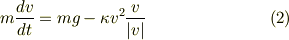
となります.ここで 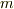 は物体の質量,
は物体の質量, 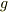 は重力加速度,
は重力加速度, 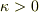 は空気抵抗の比例係数になります.
は空気抵抗の比例係数になります.
落下運動
落下時の様子を絵に描くと次図のようになります.落下運動なので 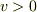 で考えます(軸を下向き正に撮っていることに注意!)
で考えます(軸を下向き正に撮っていることに注意!)
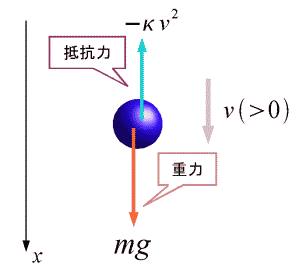
抵抗のある場合の落下
運動方程式 (2) は 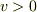 より
より
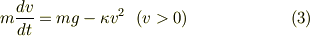
となります.抵抗力の符号は  ,つまり抵抗力は上向きに働くことになりますね.
,つまり抵抗力は上向きに働くことになりますね.
速度の時間変化を求めてみることにしましょう.(3)の両辺を 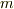 で割って,式を整理します.
で割って,式を整理します.
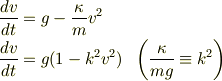
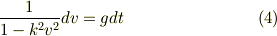
(4)を積分すれば速度変化を求めることができます. どうすれば積分を実行できるでしょうか.ここでは部分分数分解を利用することにします.
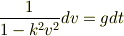
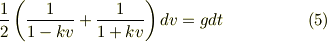
両辺を積分します.
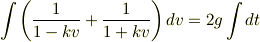
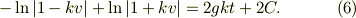
ここで 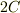 は積分定数です.
は積分定数です. 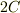 と置いたのは後々のためです.
と置いたのは後々のためです.
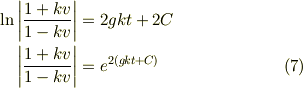
式 (7) は分母の 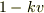 の正負によって場合分けが必要です.
の正負によって場合分けが必要です.
計算練習だと思って手を動かしてみましょう.
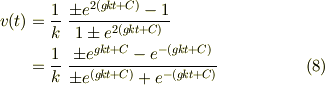
ここで 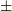 は
は 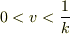 のとき
のとき 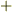 ,
, 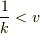 のとき
のとき  をとります.
定数
をとります.
定数 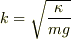 を元に戻してやると,
を元に戻してやると,
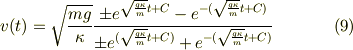
となります.
式を見やすくするために  ,
, 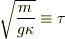 と置くことにします.
(9)式を書き直すと,
と置くことにします.
(9)式を書き直すと,
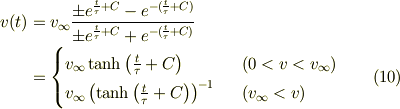
こうして 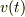 の時間変化を得ることができました.
の時間変化を得ることができました.
初期条件として 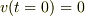 をとってやることにしましょう.
(10) で
をとってやることにしましょう.
(10) で 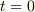 ,
,  としてやると,
としてやると,  が得られます.
が得られます.
したがって,  を初期条件にとったとき,
を初期条件にとったとき,

となります.
このときの速度の変化をグラフに書くと次のようになります.
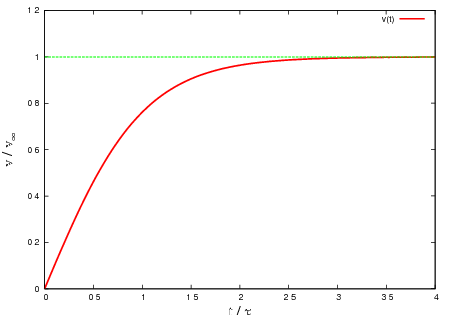
速度の変化(落下運動)
速度は時間が経過すると  へと漸近していく様子がわかります.
へと漸近していく様子がわかります.
問い 1.
抵抗力の大きさ(  )によって,終端速度
)によって,終端速度  はどう変わるでしょうか.
また終端速度に達するまでの時間スケールを表す緩和時間
はどう変わるでしょうか.
また終端速度に達するまでの時間スケールを表す緩和時間  はどうなるでしょうか.
はどうなるでしょうか.
問い 2.
式 (10) で 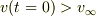 とすると,どのような v-t グラフになるでしょうか.
とすると,どのような v-t グラフになるでしょうか.
鉛直投げ上げ
おまけとして鉛直投げ上げをした場合の運動について考えてみます.やはり軸を下向き正にとっていることに注意して下さい.投げ上げなので, 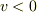 の場合を考えることになります.
の場合を考えることになります.
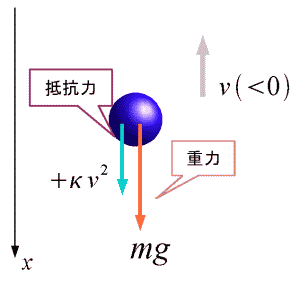
抵抗のある場合の投げ上げ
運動方程式 (2) は 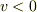 より次のようになります.
より次のようになります.
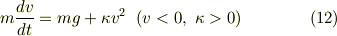
(3)との違いは,抵抗力につく符号だけです.今度は 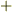 なので抵抗力は下向きにかかることになります.
(3)と同様にして解いていくことにしましょう.
なので抵抗力は下向きにかかることになります.
(3)と同様にして解いていくことにしましょう.
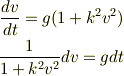
積分しましょう.
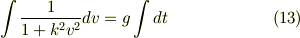
左辺の積分について考えましょう.
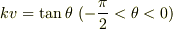 と置換すると
と置換すると 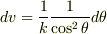 となりますので,
となりますので,

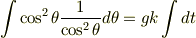
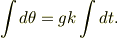
積分を実行すると,
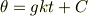
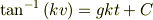
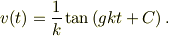
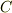 は積分定数です.
は積分定数です. 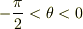 でしたから,
でしたから, 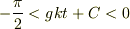 です.
先ほど定義した
です.
先ほど定義した  と
と  を用いて書くと,
を用いて書くと,
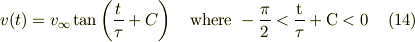
となります.
初期条件として, 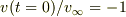 をとってみましょう.
をとってみましょう.
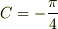 となりますので,(14)は
となりますので,(14)は
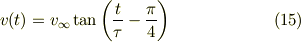
となります.
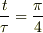 で速度が
で速度が  となり,あとは上で考えた落下運動へと移行します.
となり,あとは上で考えた落下運動へと移行します.
この様子をグラフにすると,次のようになります.赤線が速度変化を表しています.
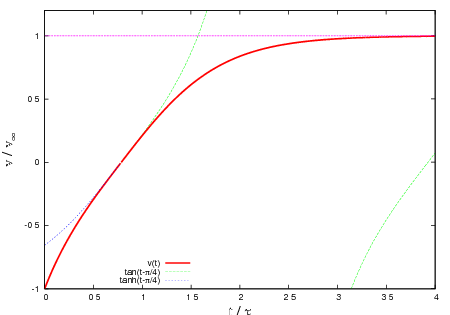
速度の変化(速度が 0 になると,最初に考えた落下運動へと移行する)
別解
「落下運動」のセクションでは部分分数分解を用いて積分を,「鉛直投げ上げ」では置換積分を行いました.
積分の形は下のように 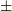 が違うだけです.
が違うだけです.
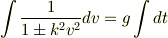
部分分数分解による方法,または置換積分による方法,どちらかだけで解けないものでしょうか. そのほうが解き方を覚えるのも楽ですよね.
落下運動
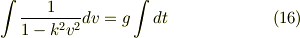
まず,落下運動を置換積分で解けないか考えてみます.
結果は(11)のようになることがすでに分かっていて,  が出てくるのでした.
が出てくるのでした.
そういえば 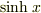 ,
, 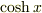 には
には 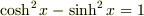 という関係があり,三角関数とよく似ています.
注目すべきは,両辺を
という関係があり,三角関数とよく似ています.
注目すべきは,両辺を 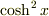 で割れば,
で割れば, 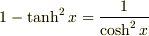 という関係が得られることです.
という関係が得られることです.
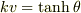 と置換してやると,うまく行きそうな気になってきませんか?やってみましょう.
と置換してやると,うまく行きそうな気になってきませんか?やってみましょう.
と,ここで注意が必要です.
 なので,全ての
なので,全ての 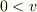 にたいして
にたいして 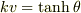 と置換するわけにはいきません.
と置換するわけにはいきません.
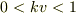 と
と 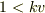 で場合分けが必要です.
で場合分けが必要です.
我々は落下運動を既に解いて,結果が (10) となることを知っています.なので  では
では 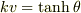 ,
, 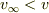 では
では 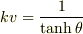 と置いてみることにします.
と置いてみることにします.
鉛直投げ上げ
では鉛直投げ上げの場合を部分分数分解を用いて積分できるでしょうか. やってみましょう. 複素数を用いて,無理矢理にでも部分分数分解してやると
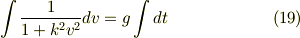

となります.積分すると
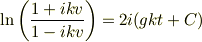
となります.ここで 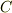 は積分定数です.
は積分定数です.  について整理してやると
について整理してやると
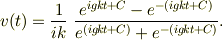
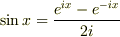 ,
, 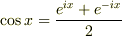 の関係を用いてやれば
の関係を用いてやれば
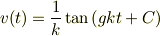
が得られます.  ,
,  を用いて書き換えると,
を用いて書き換えると,
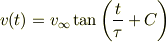
となり (14) と一致しました!
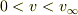 の場合
の場合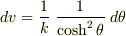 となります.
(16) は,
となります.
(16) は,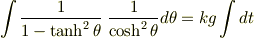
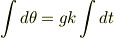
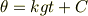
 を元に戻すと
を元に戻すと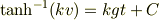
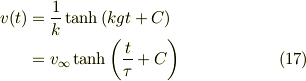
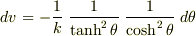 となります.
(16) は,
となります.
(16) は,