ポテンシャルとグラディエント
ベクトル解析のグラディエントってなんだか意味不明です.授業で習ってもさっぱりわかりませんでした(覚える気がなかった.だって難しいそうなんですもん).ところが最近になってやっとその便利さが分かったので,ポテンシャルエネルギーと一緒に紹介したいと思います.
ポテンシャル
なんらかの保存力が働く空間で考えます.ポテンシャルは保存力が働く空間でしか定義できません.そういう空間とは,たとえば重力場とか静電場などです.
質点 m が「ある始点」から「ある終点」に動くとき,保存力のする仕事は始点と終点のみによって決まります.質点がどこをどう通って始点から終点に移動したかは関係ないんです.ということは,位置ベクトル  の関数
の関数 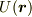 を使うとつぎのように定義できます.
を使うとつぎのように定義できます.
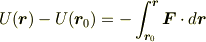
ここで始点の位置ベクトルを 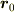 ,終点の位置ベクトルを
,終点の位置ベクトルを  としています.いきなり負号が付いてるのが気持ち悪いかもしれませんが,これは後々のつじつま合わせのためです.
としています.いきなり負号が付いてるのが気持ち悪いかもしれませんが,これは後々のつじつま合わせのためです.
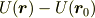
を 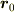 を基準にしたポテンシャルエネルギー,または位置エネルギー,もしくは単にポテンシャルといいます.さっき負号が付いていたのは,基準より下に行ったら負,上に行ったら正というふうにしたいからです.
を基準にしたポテンシャルエネルギー,または位置エネルギー,もしくは単にポテンシャルといいます.さっき負号が付いていたのは,基準より下に行ったら負,上に行ったら正というふうにしたいからです.
積分区間が始点 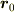 から終点
から終点  になっているのはなんとなく分かります.積分の中身
になっているのはなんとなく分かります.積分の中身
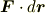
の意味は分かるでしょうか. 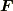 も
も  もベクトルなので,これは微小区間
もベクトルなので,これは微小区間 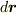 と力
と力 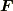 の内積をとる操作です.力と位置ベクトルの内積は仕事でしたから,積分の中身はとても小さい区間の仕事を表しています.で,積分全体では始点から終点までの仕事を足したものだということが分かります.これはポテンシャルエネルギーが仕事で蓄えられるということと一緒です.
の内積をとる操作です.力と位置ベクトルの内積は仕事でしたから,積分の中身はとても小さい区間の仕事を表しています.で,積分全体では始点から終点までの仕事を足したものだということが分かります.これはポテンシャルエネルギーが仕事で蓄えられるということと一緒です.
ポテンシャルの傾き
さて,終点の位置ベクトル  を
を 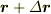 としたもの
としたもの
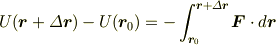
からポテンシャルエネルギーの定義
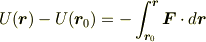
を辺々引くと 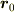 の項が消えて
の項が消えて
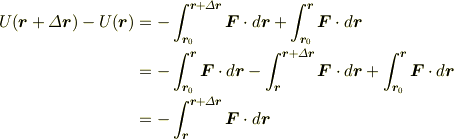
となります.位置ベクトル 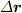 は成分で書くとつぎのように書けます.
は成分で書くとつぎのように書けます.
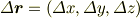
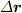 を十分小さい量とすると
を十分小さい量とすると
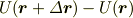
は 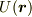 が微小区間
が微小区間 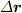 でどれだけ変化したか,という量ですから,全微分で書けます.
でどれだけ変化したか,という量ですから,全微分で書けます.
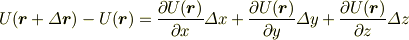
また,
![-\int_{\bm{r}}^{\bm{r}+\varDelta\bm{r}}\bm{F}\cdot d\bm{r} &= -\left[\bm{F}\cdot\bm{r}\right]_{\bm{r}}^{\bm{r}+\Delta\bm{r}}\\ &= -\left(\bm{F}\cdot(\bm{r}+\Delta\bm{r})-\bm{F}\cdot\bm{r}\right)\\ &= -\bm{F}\cdot\varDelta\bm{r}\\ &= -\left(F_x\varDelta x +F_y\varDelta y +F_z\varDelta z\right)](./1c4752b8187cfd62e3e4dd0bf4318589.png)
なのでつぎの式が得られます.
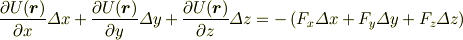
Δx,Δy,Δz の係数を比較すると
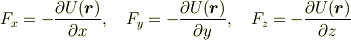
ということが分かります.これは何を表すかというと, U(r +Δr) - U(r) は U(r) の増加分で,上式はさらにその各成分の係数のマイナスですから,それぞれの成分が下向きにどれだけ傾いているか,つまり下向きの勾配を表しています.ポテンシャルの勾配とは力のことです.上の力 F の成分をベクトルで書き直すと
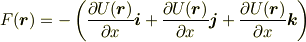
となり,勾配を表すベクトル解析の記号グラディアント
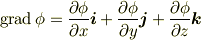
を使えばポテンシャルから受ける力 F は
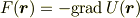
または
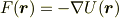
という具合に簡単に書き下すことができるようになります.この簡単な式だけでポテンシャルから受ける力は下向で,力の各成分はポテンシャルの各成分の偏微分である,ということを表現できます.こんなに簡単に書けるんならもっと早く知っときゃよかった.食わず嫌いはしないほうがいいようです.