無限小回転2
ここまで 無限小回転1 で次のようなことを勉強しました.
- 有限回転では,一般に回転の順序を変えることができないということ.
- 無限小回転においては,回転の順序を交換することができるということ.
- ベクトルを無限小回転させたときの変化分は,元のベクトルに反対称行列を掛けることによって表わされるということ.
この記事では,さらに回転についての考察を進めていきます.
ベクトルの外積を使う
読者のみなさんは,無限小回転の変化 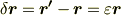 が,次のような反対称行列
が,次のような反対称行列  を使って表わされることを既に知っています.これは
を使って表わされることを既に知っています.これは  の二次以上の積が無視できることと,
の二次以上の積が無視できることと,  が直交行列であることから導き出された結果でした.
が直交行列であることから導き出された結果でした.
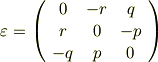
では実際に,この行列  をベクトル
をベクトル  に掛けてみることにしましょう.さぁ,どうなるでしょうか.
に掛けてみることにしましょう.さぁ,どうなるでしょうか.
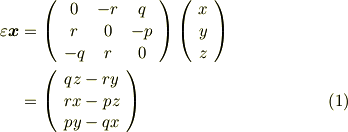
あれ!?この結果を見て,なんだかピンと来ませんか?ムムム,どこかで見たような形です.
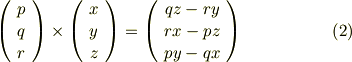
そうです.式(1)の結果は,ベクトル 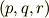 と
と 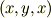 の外積と,同じになっているのです!反対称行列の積は,形式的に,ベクトルの外積に書き換えることができるということです. [*] 行列よりもベクトルの方がずっと扱いが簡単ですから,この結果は,今後の計算のためにも非常に有用だと言わねばなりません.またしても,計算が簡単になってしまいました.
の外積と,同じになっているのです!反対称行列の積は,形式的に,ベクトルの外積に書き換えることができるということです. [*] 行列よりもベクトルの方がずっと扱いが簡単ですから,この結果は,今後の計算のためにも非常に有用だと言わねばなりません.またしても,計算が簡単になってしまいました.
| [*] | 『反対称行列の代わりに外積を取るために作ったベクトル』のことを軸性ベクトル(もしくは擬ベクトル)と呼びます.例えば,この 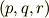 は軸性ベクトルです.軸性ベクトルではないベクトルのことを極性ベクトルと呼びます.極性ベクトルと軸性ベクトルの定義には色々ありますから,これは一つの説明の方法にすぎませんが,覚えておくといいと思います. は軸性ベクトルです.軸性ベクトルではないベクトルのことを極性ベクトルと呼びます.極性ベクトルと軸性ベクトルの定義には色々ありますから,これは一つの説明の方法にすぎませんが,覚えておくといいと思います. |

実は, 無限小回転1 の最後で,行列  の成分をこのような形に置いたのは,行列
の成分をこのような形に置いたのは,行列  と,ベクトル
と,ベクトル 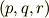 の外積とを,対応を見やすくするためだったのです.ここで作ったベクトル
の外積とを,対応を見やすくするためだったのです.ここで作ったベクトル 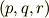 を,とりあえず
を,とりあえず  と名づけることにします.
と名づけることにします. 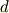 がついているのは,微小だよ,ということを意味するためのもので,何かの微分になっているという意味ではないことに注意してください.
がついているのは,微小だよ,ということを意味するためのもので,何かの微分になっているという意味ではないことに注意してください.
無限小回転はベクトルのように考えてよい
ベクトルを無限小回転させるとき,その変化分を,ベクトルの外積によって表わすことが出来るということでした. ところが,ベクトル 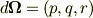 というのは,式(3)が成り立つように,反対称行列の3つの成分を,いわば作為的に並び替えて,強引にこしらえたベクトルですから,私達は,その一つ一つの成分の物理的意味を十分検討したとは言えません.
というのは,式(3)が成り立つように,反対称行列の3つの成分を,いわば作為的に並び替えて,強引にこしらえたベクトルですから,私達は,その一つ一つの成分の物理的意味を十分検討したとは言えません.
ベクトル  の個々の成分の意味を考えるために,試しに
の個々の成分の意味を考えるために,試しに 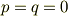 とし,ベクトル
とし,ベクトル 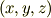 との外積を考えてみます.
との外積を考えてみます.
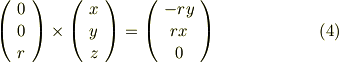
この結果を図形的に考えて見ましょう.
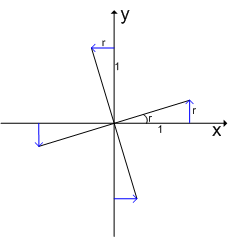
式(4)より,  方向には
方向には 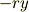 ,
,  方向には
方向には 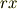 の変化があるということですから,
の変化があるということですから,  軸,
軸,  軸がそれぞれ図に青い矢印で示したように,半時計回りに角度
軸がそれぞれ図に青い矢印で示したように,半時計回りに角度 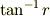 だけ回転をするということです.この回転角はいま微小だと考えていますので,
だけ回転をするということです.この回転角はいま微小だと考えていますので, 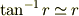 が成り立ちます.
が成り立ちます.
こうして,  の
の  成分
成分  は,
は,  軸回りの微小回転角を表しているということが分かりました.同様にして
軸回りの微小回転角を表しているということが分かりました.同様にして  ,
,  もそれぞれ
もそれぞれ  軸,
軸,  軸まわりの微小回転角を表していることが分かります.
軸まわりの微小回転角を表していることが分かります.
ベクトル  の各成分は,各軸回りの微小回転角を表しているというのですから,これは驚くほど分かりやすい結果です.(回転の方向は,それぞれの軸で,右ネジが進むように回す向き,つまり次の図にあるような向きです.)
の各成分は,各軸回りの微小回転角を表しているというのですから,これは驚くほど分かりやすい結果です.(回転の方向は,それぞれの軸で,右ネジが進むように回す向き,つまり次の図にあるような向きです.)
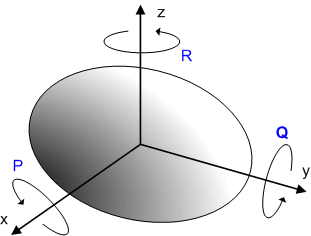
それぞれ個別の微小回転は,基底ベクトルを使えば, 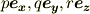 と書けます.
と書けます.  は,これら個別の微小回転の和になっていると考えることも出来るでしょう.
は,これら個別の微小回転の和になっていると考えることも出来るでしょう.
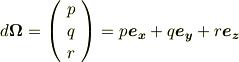
微小回転をベクトルで表現できることの最大の利点は,ベクトルの加法・減法が応用できるということです.例えば,剛体に二つの微小回転 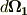 と
と 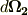 が行われる場合,これをベクトルのように足してしまって良いということです.
が行われる場合,これをベクトルのように足してしまって良いということです.
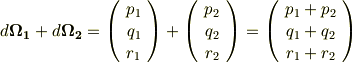
もしくは,何らかの複合的な微小回転  が行われているとき,これをベクトルの成分に分解して考えてもいい,ということでもあります.
が行われているとき,これをベクトルの成分に分解して考えてもいい,ということでもあります.
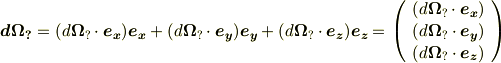
このようにして,任意の微小回転を,基本となる,座標軸回りの微小回転を使って表現できるのです.有限回転では,そんなに簡単に回転を組み合わせることが出来なかったことを思い出してください.『無限小回転はベクトルと見なせる』,これは非常に感動的な結果です. [†]
| [†] | ここで出てきた  は,全て微小量を成分とするようなベクトルです.これは微分ベクトルと呼ばれるもので, は,全て微小量を成分とするようなベクトルです.これは微分ベクトルと呼ばれるもので,  の前に の前に 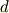 がついているのも,微分ベクトルだということを表しているのです.さて,一般の微分ベクトルには,その母関数となるベクトル(それを微分すると微分ベクトルになる)が存在することが多いのですが,注意しなければならないのは, がついているのも,微分ベクトルだということを表しているのです.さて,一般の微分ベクトルには,その母関数となるベクトル(それを微分すると微分ベクトルになる)が存在することが多いのですが,注意しなければならないのは,  が『何かの微分ではない』ということです.微分の計算を思い出してください.何か有限の量があり,それが微分可能なとき,その量の微分が導き出せる,というのが普通の手順でした.しかし,読者のみなさんが既に見たように,有限回転は単一のベクトルでは表せません.(ベクトルの有限回転を表すには,複数のベクトルが必要です.くわしくは ベクトルの回転 を参照して下さい.)すなわち,無限小回転は有限回転の微分にはなっていないわけです. が『何かの微分ではない』ということです.微分の計算を思い出してください.何か有限の量があり,それが微分可能なとき,その量の微分が導き出せる,というのが普通の手順でした.しかし,読者のみなさんが既に見たように,有限回転は単一のベクトルでは表せません.(ベクトルの有限回転を表すには,複数のベクトルが必要です.くわしくは ベクトルの回転 を参照して下さい.)すなわち,無限小回転は有限回転の微分にはなっていないわけです.  は微分ベクトルですが,それは大きさが微小であるというだけであって,何かの微分によって導かれたものではないのです.用語や記号が紛らわしいのが一番の問題ですね. は微分ベクトルですが,それは大きさが微小であるというだけであって,何かの微分によって導かれたものではないのです.用語や記号が紛らわしいのが一番の問題ですね. |
ベクトルの微小回転が,外積を使った形で表せるというのは, ベクトルの回転 の記事で求めた結果に一致しています. ベクトルの回転 では,まずベクトルの有限回転の式を考え,しかるのちに,回転角を微小だと近似して(微分ではないことに注意!),同様の結果を得たのでした.少しアプローチが違いますが,同じ式に帰着しています.(当然といえば当然ですね)
まとめ
ここまでに,随分と色々な結果を得ました.
- 有限回転では回転の順序は交換不可能であったが,微小回転においては回転の順序が交換可能である.
- 有限回転を表現するには一般に
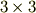 (
( 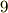 成分)の行列が必要であったが,微小回転を表わすには,たった
成分)の行列が必要であったが,微小回転を表わすには,たった 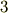 成分で十分である.
成分で十分である. - 微小回転は反対称行列(
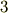 成分)によって表わされた.
成分)によって表わされた. - 微小回転を表すには,行列の代わりにベクトルの外積を使っても良い.
- 微小回転は,有限回転の微分ではない.
- 微小回転は,ベクトルのように扱って良い.(ベクトルの合成・分解が使える.)
物理学では色々な分野で,何か物理量の変化を記述するために様々な方程式が出てきますが,その多くは微分方程式の形をしています.微分方程式とは『何かがちょこっと変わったときに,他の量もちょこっと変わる』という関係を表現するものでした.ですから,角度の変化を微分の形で表すときに,微小回転(ちょこっとした回転)という概念が出てくるのは,たいへん自然なことだと言えるでしょう.(  は何かの微分ではないと書きましたが,これを微小時間
は何かの微分ではないと書きましたが,これを微小時間 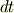 で割ったもの
で割ったもの 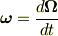 は微分になります.この後の計算に出てくるのは,主に
は微分になります.この後の計算に出てくるのは,主に 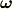 ですから微積分がバリバリ使えます.) [‡]
ですから微積分がバリバリ使えます.) [‡]
| [‡] | 微分を本格的に使い始めたのはニュートンですが,微分方程式を使う方法があまりにも便利で強力なため,その後,物理学は微分方程式を使うという枠組みを主流に発展してきた感があります.微分方程式は非常に強力な道具ではありますが,それが全てではありません.あくまでも,一つの記述の仕方に過ぎません.例えば,セル・オートマトン理論と言うものによれば,微分とは関係のない,非常に単純なルールだけに支配される系が,交通渋滞や動植物の動き,流体力学などを非常に美しく記述することが分かってきました.全然違ったルールで記述される力学もあるわけです. |
このように,微小回転という概念が,物理学の基礎方程式に出てくるのは自然のなりゆきと言えます.しかし,微小回転に関して,今まで見てきたような,計算に便利な様々な性質があるというのは,決して自然のなりゆきではありません.例えば,有限長さ 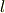 と微小長さ
と微小長さ 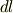 を考えてみると,
を考えてみると, 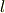 と
と 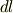 の間にとりわけ幾何学的な性質の違いはありません.有限量と無限小の量とに間に,常に幾何学的な性質の違いが生ずるわけではないのです.私達は微小回転に関して大変幸運だった(?)と言えるでしょう.
の間にとりわけ幾何学的な性質の違いはありません.有限量と無限小の量とに間に,常に幾何学的な性質の違いが生ずるわけではないのです.私達は微小回転に関して大変幸運だった(?)と言えるでしょう.