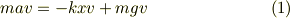力学的エネルギー保存則の導出
力学的エネルギー保存則を運動方程式から導いてみましょう.
- 運動方程式を立てる
- 両辺に速度の成分を掛ける
- 両辺を微分の形で表す
- イコールゼロの形にする
という手順で導きます.
両辺を微分の形で表す
式(1)は
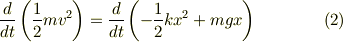
と微分の形で表すことができます.左辺は運動エネルギー,右辺第一項はバネの位置エネルギー(の符号が逆になったもの),右辺第二項は重力の位置エネルギー(の符号が逆になったもの),のそれぞれ時間微分の形になっています.なぜこうなるのかを説明します.
加速度  と速度
と速度  はそれぞれ
はそれぞれ
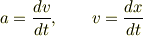
という関係にあります.加速度は速度の時間微分,速度は位置の時間微分です.この関係を使って計算すると式(2)の左辺は
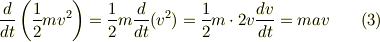
となります.ここで1行目から2行目のところで合成関数の微分公式を使っています.式(3)は式(1)の左辺と一緒ですね.運動方程式に速度  をあらかじめ掛けておいたのは,このように運動方程式をエネルギーの微分で表すためです.同じように計算していくと式(2)の右辺の第1項は
をあらかじめ掛けておいたのは,このように運動方程式をエネルギーの微分で表すためです.同じように計算していくと式(2)の右辺の第1項は
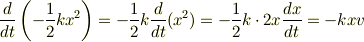
となり,式(2)の右辺第1項と同じになります.第2項は
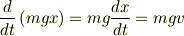
となり,式(1)の右辺第2項と同じになります.
なんだか計算がごちゃごちゃしてしまいましたが,式(1)と式(2)が同じものだということがわかりました.これが言いたかったんです.
イコールゼロの形にする
式(2)の右辺を左辺に移項すると
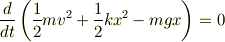
という形になります.この式は何を意味しているでしょうか.カッコの中身はそれぞれ運動エネルギー,バネの位置エネルギー,重力の位置エネルギーを表しているのでした.
それらを全部足して,時間微分したものがゼロになっています.ということは,エネルギーの合計は時間的に変化しないことになります.つまりエネルギーの合計は常に一定になるので,エネルギーが保存されるということがわかります.
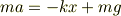
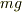 とばねの力
とばねの力 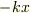 が働いている物体(質量は
が働いている物体(質量は 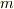 )の運動方程式です.
)の運動方程式です.