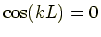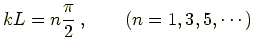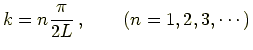式 (
7.17) の
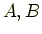
は境界条件,規格化条件から決まる定数である.
まずは境界条件から考えよう.
ポテンシャル
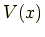
は式 (
7.8.1) で定められていた.
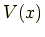
は
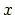
が
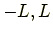
の場所から無限大になる.
ここで重要なのは
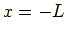
および
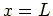
の場所でポテンシャルが無限,
つまり粒子が存在できないということ.
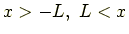
の場合に
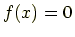
となるのは
ポテンシャル
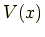
の値で場合分けしたときすでに考えた.
しかしシュレディンガー方程式の解である波動関数は連続でなければならないから,
ちょうど境界にあたる
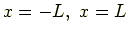
の部分では
式(
7.12)もこの条件を満たさなければならない.
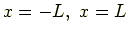 で粒子は存在できないのだから,
この範囲の
で粒子は存在できないのだから,
この範囲の 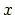 で式(7.17)の
で式(7.17)の 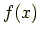 はゼロになる.したがって
はゼロになる.したがって
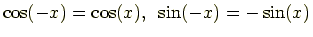
という関係を使うと,
この式から
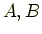
の値を決めることができる.
まず
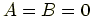
という場合が考えられるが,
この場合は無意味なので考えない.
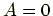 の場合
の場合
式 (7.20), (7.21) の辺々を引くと
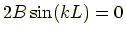 ,
,
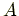 と
と 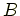 は両方ともゼロにはならないので,
は両方ともゼロにはならないので,
したがって
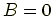 の場合
の場合
式 (7.20), (7.21) の辺々を足すと
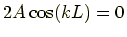 ,
,
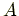 と
と 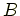 は両方ともゼロにはならないので,
は両方ともゼロにはならないので,
したがって
両方の場合をまとめると
となる.
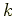
はこのように許される値が決まってしまった.
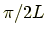
の
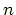
倍になっている.飛び飛びなわけだ.
この飛び飛びの状態を量子化
されているといい,
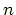
を量子数
と呼ぶ.
物理のかぎプロジェクト / 平成18年3月2日
![]() で粒子は存在できないのだから,
この範囲の
で粒子は存在できないのだから,
この範囲の ![]() で式(7.17)の
で式(7.17)の ![]() はゼロになる.したがって
はゼロになる.したがって
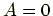 の場合
の場合
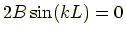 ,
,
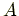 と
と 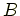 は両方ともゼロにはならないので,
は両方ともゼロにはならないので,
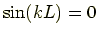
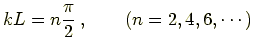
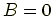 の場合
の場合
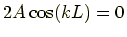 ,
,
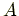 と
と 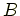 は両方ともゼロにはならないので,
は両方ともゼロにはならないので,