イデアルによる類別
この記事では, テンソル代数 から外積代数を作れることを勉強します.テンソル代数は 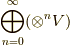 と表現される,ベクトル代数
と表現される,ベクトル代数 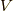 からテンソル積と直和によって生成される代数でした.無限次元のベクトル空間
からテンソル積と直和によって生成される代数でした.無限次元のベクトル空間  までを含んでいます.テンソル計算を全てカバーする空間という意味では,テンソル代数を考えた意義はありますが,無限階のテンソルとは,いかにも使い勝手が悪そうに聞こえます.
までを含んでいます.テンソル計算を全てカバーする空間という意味では,テンソル代数を考えた意義はありますが,無限階のテンソルとは,いかにも使い勝手が悪そうに聞こえます.
一方,外積代数は  次元のベクトル空間
次元のベクトル空間 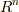 から構成する場合,高々
から構成する場合,高々  階の外積空間
階の外積空間 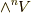 まで出てきませんから,実用上手軽そうです.しかも,各外積空間の次元も
まで出てきませんから,実用上手軽そうです.しかも,各外積空間の次元も 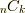 と,そんなに大きくはなく,
と,そんなに大きくはなく, 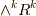 と
と 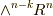 にはホッジ作用素という同型写像までありましたから,実用面の扱いはかなり楽そうです.実は,テンソル空間をグループ分け( 類別 といいます)することで,外積代数を作ることができるのです.(
にはホッジ作用素という同型写像までありましたから,実用面の扱いはかなり楽そうです.実は,テンソル空間をグループ分け( 類別 といいます)することで,外積代数を作ることができるのです.( 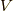 が
が  次元のベクトル空間ならば,
次元のベクトル空間ならば,  個に分類することになります.)
個に分類することになります.)
代数的な知識がある程度必要になります.特に, 類別 , 剰余類 , 剰余類2 , イデアル , テンソル代数 の内容が前提になります.自信のない人は,先にこれらの記事を復習しておくことをお勧めします. 外積代数なんてどっから出てきたんだ?という点に興味が無い人は,本稿から「イデアルで外積代数を入れる3」までを飛ばして,微分形式へ進んで下さい.
| [*] | テンソル代数から,イデアルによる類別という操作によって外積代数は作れるわけですから,外積代数をテンソル代数の特殊な場合として,テンソル代数に含めてしまうことは可能です.そのような意味では,外積代数(そして,その応用である微分形式も)は,テンソル解析の一分野だとも言えます.実際,外積代数はテンソル積に交代性を付け加えたものだと見ることもできて,交代形式のテンソル代数と呼ぶことも可能です.このような立場から書かれた本では,テンソルの話の延長として外積代数が出てきます.一方,微分形式の応用的な有用性に力点を置いた本では,テンソルの話は省略して,いきなり外積代数の演算構造から書かれていたりします.(さらに,外積代数も飛ばして,微分形式から書き始めている本もあります.)色々な立場の人がいると思いますが,単に面白いので,イデアルによる類別の話も取り上げます.もっとも,商代数を取るという考え方は,いずれコホモロジーという概念を考えるときなどに使いますので,馴れておくと良いと思います. |
イデアルによる類別
あるベクトル空間 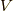 がイデアル
がイデアル 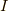 を持つとします.(ベクトル空間は 環 になり, イデアル とは一種の部分環のことでした. ベクトルの割り算 も参照下さい.)
を持つとします.(ベクトル空間は 環 になり, イデアル とは一種の部分環のことでした. ベクトルの割り算 も参照下さい.) 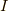 を使って,
を使って, 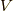 に含まれる二つの元
に含まれる二つの元 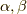 の間に次のような同値関係を入れることが出来ます.(同値関係については 剰余類2 参照.)
の間に次のような同値関係を入れることが出来ます.(同値関係については 剰余類2 参照.)
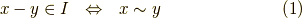
まず,式 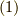 が確かに同値関係であることを確認しましょう.
が確かに同値関係であることを確認しましょう.
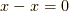 ですが,
ですが, 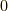 は何に掛けても
は何に掛けても 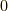 ですから,常にイデアルの元です.
ですから,常にイデアルの元です. 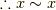 (反射律)
(反射律)- 定義より
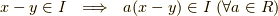 ですが,
ですが,  として
として  を考えると
を考えると 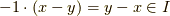 が示されます.
が示されます. 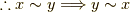 (対称律)
(対称律) 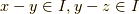 ならば,
ならば, 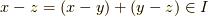 が言えます.(推移律)
が言えます.(推移律)
反射律,対称律,推移律が満たされましたので,式 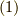 は確かに同値関係を与えています.集合の元に同値関係が与えられれば,元を類別することが出来るのでした.( 類別 参照.)
は確かに同値関係を与えています.集合の元に同値関係が与えられれば,元を類別することが出来るのでした.( 類別 参照.)
![V = \{ x,y,z,....\} \ \Longrightarrow \ V/I = \{ [x],[y],[z],... \}](./c0f80012210f58d05a8ca32db9cd17d6.png)
イデアルによる 商集合 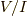 の各類は,しばらく
の各類は,しばらく ![[ \ \ ]](./cc982a1be60f2b0a6827ce33f75e951d.png) で表わすことにします.ここまでは,代数学を多少とも勉強したことのある人ならば難しくはなかったと思いますが,代数学を全然勉強したことのない人にとってはチンプンカンプンだったかも知れません.よく分からなかった人は,これを機会に 代数学 を一から勉強してみるのも良いでしょう.この記事で,代数学のページに書いてある内容を再び詳しく説明することはしません.
で表わすことにします.ここまでは,代数学を多少とも勉強したことのある人ならば難しくはなかったと思いますが,代数学を全然勉強したことのない人にとってはチンプンカンプンだったかも知れません.よく分からなかった人は,これを機会に 代数学 を一から勉強してみるのも良いでしょう.この記事で,代数学のページに書いてある内容を再び詳しく説明することはしません.
イデアルによる商集合からベクトル空間を作る
ベクトル空間 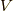 には元の間に何らかの乗法も定義されているとします.(乗法の定義されたベクトル空間を代数と呼ぶのでした.)
には元の間に何らかの乗法も定義されているとします.(乗法の定義されたベクトル空間を代数と呼ぶのでした.) 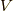 からイデアル
からイデアル 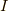 によって作った商集合
によって作った商集合 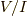 も,各同値類の間に次のように,加法,スカラー積,乗法を導入することで代数になることが示せます.
も,各同値類の間に次のように,加法,スカラー積,乗法を導入することで代数になることが示せます.
![[x]+[y]=[x+y]](./8e638b528cb3eddd7763c689a0e860fc.png) (加法)
(加法)![a[x]=[ax]](./ec7e980edef002f7ebecabf61a8026c3.png) (スカラー積)
(スカラー積)![[x][y]=[xy]](./678a9f2474dd97aa24b096bc956e821d.png) (乗法)
(乗法)
本当に 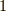 〜
〜 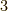 のような規則が成り立っていると言えるのかは,ちょっと見ただけでは自明ではありませんので,以下に簡単に示すことにします.
のような規則が成り立っていると言えるのかは,ちょっと見ただけでは自明ではありませんので,以下に簡単に示すことにします.
【加法】
proof
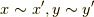 とすると,定義より
とすると,定義より 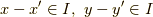 です.このとき,
です.このとき, 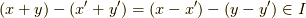 となるので,
となるので, 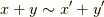 が言えます. ■
が言えます. ■
【スカラー積】
proof
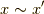 とすると,定義より
とすると,定義より 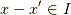 です.さらにイデアルの定義より
です.さらにイデアルの定義より 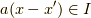 ですが,右辺を展開すれば
ですが,右辺を展開すれば 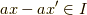 で,
で, 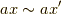 が示されます.■
が示されます.■
【乗法】
proof
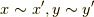 とすると,定義より
とすると,定義より 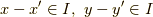 です.このとき,
です.このとき, 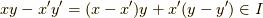 となるので,
となるので, 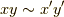 が示されます.■
が示されます.■
確かに, 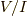 の元(つまり同値類ですね)の間にも,加法,スカラー積,乗法の三つの演算が定義できています.イデアルによって作った
の元(つまり同値類ですね)の間にも,加法,スカラー積,乗法の三つの演算が定義できています.イデアルによって作った 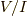 のような代数を 商代数 と呼びます.
のような代数を 商代数 と呼びます.
Important
代数 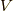 のイデアル
のイデアル 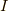 による商集合
による商集合 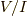 は,代数になります.
は,代数になります.
( イデアルで外積代数を入れる1 に続きます.)