補間法：ラグランジュ補完

天気図の等圧線を描くプログラムをつくりたくて補間法を少しずつ勉強したことがあります．これはそのときのメモです．その補間法，数値計算のどの本を見ても一番最初に載っているものがラグランジェ補間です．一番かんたんなアルゴリズムで，補間法というにはあまりにも補間してくれませんが，とりあえずプログラムを書いてみました．

アルゴリズム

n + 1 個の離散点（とびとびの点）

$\displaystyle x_0,x_1,x_2,\dots,x_n$

があったとします．この離散点を滑らかにつなげたい（補間したい）わけです．これらの離散点は

$\displaystyle x_0 < x_1 < x_2 < \dots < x_n$

というふうに昇順に整列されているとします．整列されていなければ整列しておきます．つぎに，これら全ての離散点を通る関数を P(x) とします．この P(x) が補完曲線になります．点列

$\displaystyle (x_i,f_i) ,\quad (i=0,1,2,\dots,n)$

に対し n + 1 次多項式 L(x) と，n 次多項式 g(x) をつぎのように定義します．

$\displaystyle L(x)$	$\displaystyle = (x-x_0)(x-x_1)\cdots(x-x_n)$
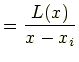
$\displaystyle g_i(x)$	$\displaystyle =\frac{L(x)}{x-x_i}$

このとき，補間曲線 P(x) は

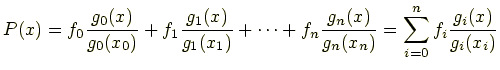
$\displaystyle P(x)=f_0\frac{g_0(x)}{g_0(x_0)}+f_1\frac{g_1(x)}{g_1(x_1)} +\cdots +f_n\frac{g_n(x)}{g_n(x_n)}= \sum^n_{i=0}f_i\frac{g_i(x)}{g_i(x_i)}$

で書ける，というのがラグランジュ補完のアルゴリズムです．

コーディング

上のアルゴリズムをもとに，試しに書いてみたラグランジェ補間法のコードです．試しなのでおかしなところがあります．例えば x の始点で値が変になるところなどです．

[lag_hokan.c]

#include <stdio.h>

int main(void) {
  int n, i, j, m;
  double GiXi[100], FG[100], x[100], f[100], X, Kx=0, Lx=1, Px;
  FILE *fp;
  
  fp = fopen("lag.dat", "w");

  /* 補間用データ */
  n = 5;  /* lagrange多項式の次元 */
  m = 6;  /* データの数 */
  x[0] = 0.1;
  x[1] = 2.1;
  x[2] = 4.0;
  x[3] = 5.9;
  x[4] = 7.1;
  x[5] = 9.2;
  
  f[0] = 3.0;
  f[1] = 5.5;
  f[2] = 21.0;
  f[3] = 52.0;
  f[4] = 26.0;
  f[5] = 3.0;
  
  /* 先にデータの数 m だけ Gi(Xi) を求める */
  for (i=0; i<m; i++) {
    GiXi[i] = 1;
    for(j=0 ; j<=n ; j++){
      if (i==j) GiXi[i] = GiXi[i];
      else GiXi[i] = GiXi[i] * (x[i]-x[j]);
    }
    FG[i] = f[i] / GiXi[i];
  }
  
  /* X の範囲だけ補間値の計算 */
  for(X=0.1 ; X<=10.0 ; X = X+0.02){
    Kx = 0;
    Lx = 1;
    /* Kx の計算 */
    for (i=0; i<m; i++) {
      if (x[i]!=X) Kx = Kx+FG[i] / (X-x[i]);
    }
    /* Lx の計算 */
    for (i=0; i<=n; i++) {
      if (x[i]!=X) Lx = Lx * (X-x[i]);
    }
    /* Px の計算 */
    Px = Lx * Kx;

    /* X 座標と Px をファイル lag.dat に出力 */
    fprintf(fp, "%f %f\n", X, Px);
  }
  
  return 0;
}

結果と考察

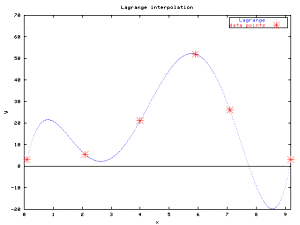
プログラムを実行するとlag.datという P(x) の (x, y) 座標の入ったデータファイルができるので，Gnuplotでグラフにするとつぎのようになりました（クリックで拡大）．

5次のラグランジェ多項式を使ったので極値が4つあります．一応全てのポイントを通ってはいるのですが，各データポイントの間がずいぶん波打っています．特に両端で顕著に波打ちが見られます．最初に書いたように，天気図の等気圧点（等圧線）を描きたくて補間法のプログラムをつくりましたが，こんなに波打っていたのではまともな等圧線は描けそうにありません．ラグランジェ補間は天気図作成には向いていないということがわかりました．

[home] [計算物理学] [ページの先頭]