調和振動子ポテンシャルの数値解
home > 計算物理学 >目次
調和振動子ポテンシャル
解析的に固有値が求められる調和振動子ポテンシャルで数値解を求め、 解析解と比較してみます。一次元調和振動子のシュレディンガー方程式は
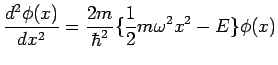
です。この調和振動子の解析解はよく知られていて、次のようになっています。
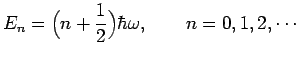
なるべく式を簡単にしたいので、
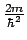 =1,
=1,
![]() =1
として計算します。するとするとポテンシャルは
=1
として計算します。するとするとポテンシャルは
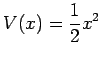
となります。また、
![]() は
は
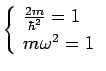
より
![]() となります。だから固有値は
となります。だから固有値は
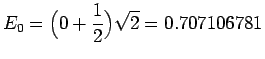
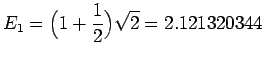
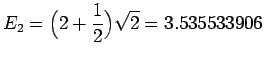
と求まります。数値計算した結果がこの解析解の固有値とどれくらい差があるかを調べて、 数値計算の精度を求めてみます。
コーディング
アルゴリズム
微分方程式を解くアルゴリズムには ルンゲ・クッタ法 を使っています。 まず適当な E を与たシュレディンガー方程式(微分方程式)を解き、 波動関数 φ(x) が x→∞ で +∞ に発散する場合は E を少し増加(E + dE)させてもう一度微分方程式を解きます。
E を増加させながら微分方程式を解くことを繰り返し、 発散が +∞ から -∞ に変わったら E を減少させます。 このとき、減少の度合はいままでの 10分の1 にします(E - dE/10)。
E を減少させながらまた微分方程式を解いていき、 発散が -∞ から +∞ に変わったら E を増加させます。 増加の度合はさらに 10分の1 にします(E + dE/100)。 この操作を繰り返し、 +∞になるEと、 -∞になるEとのはさみ撃ちで 固有関数 E を決めていきます。つぎのようなイメージです.
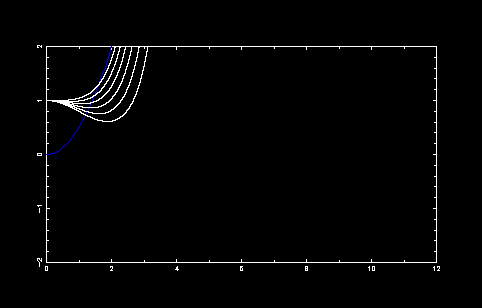
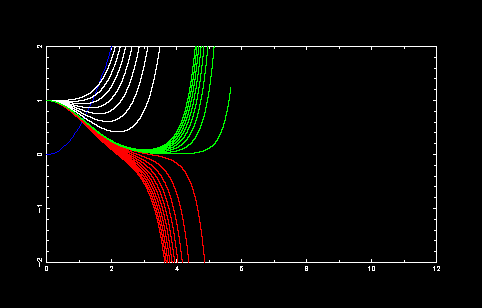
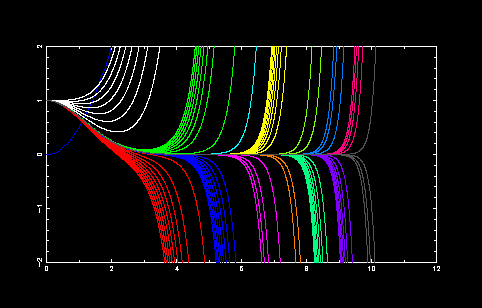
固有関数 E が収束していく様子です.発散の符号が変化したところで色を変えています. だんだん x→∞ で 0 に近づいていることに注目してください. ただ,誤差がたまってくるのでどうしても途中で発散してしまいます.
ソースコード
1 /* =====================================================================
2 ルンゲ・クッタ法で一次元調和振動子ポテンシャルの固有値を求める
3 Last modified: Oct 20 2003
4 ===================================================================== */
5
6
7
8 #include <stdio.h>
9 #include <math.h>
10 #include "cpgplot.h"
11
12
13
14 // 物理設定
15 double E = 0.0;
16 double dE = 1.0;
17 int parity = 1;
18
19 // きざみ幅
20 double h = 0.001;
21
22
23
24 /* ---------------------------------------------------------------------
25 potential function
26 --------------------------------------------------------------------- */
27
28 double V(double x) // V(x)=1/2*x^2
29 {
30 return (pow(x,2)/2);
31 }
32
33
34
35 /* ---------------------------------------------------------------------
36 導関数の定義
37 --------------------------------------------------------------------- */
38
39 double dphi(double x, double phi, double z) // dphi/dx = z
40 {
41 return(z);
42 }
43 double dz(double x, double phi, double z) // dz/dx = (V(x)-E)phi
44 {
45 return( (V(x) - E) * phi );
46 }
47
48
49
50 /* ---------------------------------------------------------------------
51 ルンゲ・クッタ法
52 --------------------------------------------------------------------- */
53
54 void rungeKuttaMethod(double x0, double phi0, double z0, double h){
55 int i, j, n, loop, color;
56 double x, phi, z, k[4], q[4], phi_old[2];
57 loop = 15/h; color = 9;
58
59 for(n=1 ; n<=14 ; n++){
60 dE = -1 * dE/10;
61 x = x0; phi = phi0, z = z0; // 波動関数初期化
62
63 while(1){
64 for(i=1 ; i<=loop ; i++){
65 // 4次のRunge-kutta法 の連立
66 k[0] = h * dphi(x, phi, z);
67 q[0] = h * dz(x, phi, z);
68 k[1] = h * dphi(x + h/2, phi + k[0]/2, z + q[0]/2);
69 q[1] = h * dz(x + h/2, phi + k[0]/2, z + q[0]/2);
70 k[2] = h * dphi(x + h/2, phi + k[1]/2, z + q[1]/2);
71 q[2] = h * dz(x + h/2, phi + k[1]/2, z + q[1]/2);
72 k[3] = h * dphi(x + h, phi + k[2], z + q[2]);
73 q[3] = h * dz(x + h, phi + k[2], z + q[2]);
74 phi += k[0]/6 + k[1]/3 + k[2]/3 + k[3]/6;
75 z += q[0]/6 + q[1]/3 + q[2]/3 + q[3]/6;
76 x = x0 + i * h;
77 }
78
79 // 今回と前回のphiを保存
80 phi_old[0] = phi_old[1]; phi_old[1] = phi;
81
82 // 今回と前回のphiが異符号ならwhile(1)を抜ける
83 // i=1ではphi_oldの値が無意味なので比較しない
84 if ( (i>=2) && ((phi_old[0] > 0) && (phi < 0)) ) break;
85 if ( (i>=2) && ((phi_old[0] < 0) && (phi > 0)) ) break;
86
87 printf("%2.15lf\n", E); // モニタ
88 E += dE; // 固有値変更
89 x = x0; phi = phi0, z = z0;
90 }
91 }
92
93 // 求まった固有値を表示
94 printf("E = %2.15lf\n", E);
95
96 // 波動関数の描画
97 x = x0; phi = phi0, z = z0;
98 for(i=1 ; i<=loop ; i++){
99 k[0] = h * dphi(x, phi, z);
100 q[0] = h * dz(x, phi, z);
101 k[1] = h * dphi(x + h/2, phi + k[0]/2, z + q[0]/2);
102 q[1] = h * dz(x + h/2, phi + k[0]/2, z + q[0]/2);
103 k[2] = h * dphi(x + h/2, phi + k[1]/2, z + q[1]/2);
104 q[2] = h * dz(x + h/2, phi + k[1]/2, z + q[1]/2);
105 k[3] = h * dphi(x + h, phi + k[2], z + q[2]);
106 q[3] = h * dz(x + h, phi + k[2], z + q[2]);
107 cpgsci(color); cpgmove(x, phi); cpgdraw(x + h/6, phi + k[0]/6);
108 cpgsci(color); cpgmove(x + h/6, phi + k[0]/6); cpgdraw(x + h/2, phi + k[1]/2);
109 cpgsci(color); cpgmove(x + h/2, phi + k[1]/2); cpgdraw(x + h*5/6, phi + k[2]*5/6);
110 cpgsci(color); cpgmove(x + h*5/6, phi + k[2]*5/6); cpgdraw(x + h, phi + k[3]);
111 phi += k[0]/6 + k[1]/3 + k[2]/3 + k[3]/6;
112 z += q[0]/6 + q[1]/3 + q[2]/3 + q[3]/6;
113 x = x0 + i * h;
114 }
115 }
116
117
118
119 /* ---------------------------------------------------------------------
120 調和振動子ポテンシャルの描画(青線) V(x)=1/2(x)
121 --------------------------------------------------------------------- */
122
123 void DrawPotential(double xmax)
124 {
125 double i;
126 cpgsci(4); cpgslw(1);
127 cpgmove(-xmax, pow(xmax,2)/2);
128 for(i = -xmax ; i < xmax ; i += 0.1){
129 cpgdraw( i, pow(i,2)/2 );
130 }
131 }
132
133
134
135 /* ---------------------------------------------------------------------
136 main
137 --------------------------------------------------------------------- */
138
139 int main(void)
140 {
141 double phi0, z0;
142 double xmax, bottom, top;
143
144 // グラフ描画設定
145 xmax = 12.0;
146 bottom = 2.0;
147 top = 2.0;
148
149 cpgopen( "/xserv" );
150 cpgpap( 8.0, .6 );
151 cpgenv( 0, xmax, -bottom, top, 0, 0 );
152
153 if(parity == -1){ // 奇関数
154 phi0 = 0.0; z0 = 1.0;
155 }
156 else{ // 偶関数
157 phi0 = 1.0; z0 = 0.0;
158 }
159
160 DrawPotential(xmax);
161 rungeKuttaMethod(0.0, phi0, z0, h);
162
163 cpgclos();
164
165 return 0;
166 }
実行結果
プログラム 15 〜 17 行目の E, dE, parity の値を変更しながら, 基底状態〜第 9 励起状態まで求めました. ルンゲ・クッタ法のきざみ幅 h はすべて 0.001 で計算しています.
基底状態
初期設定: double E = 0.0; double dE = 1.0; int parity = 1;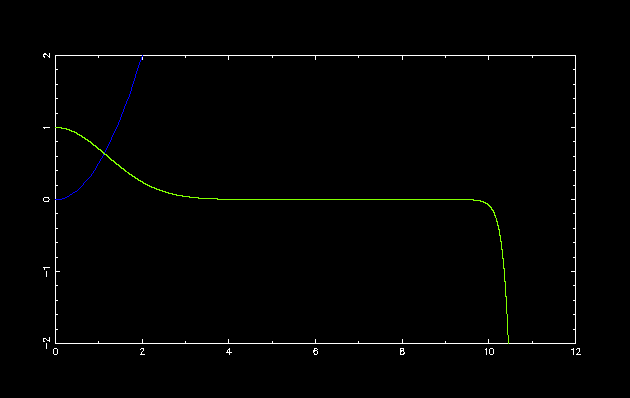
第 1 励起状態
初期設定: double E = 2.0; double dE = 1.0; int parity = -1;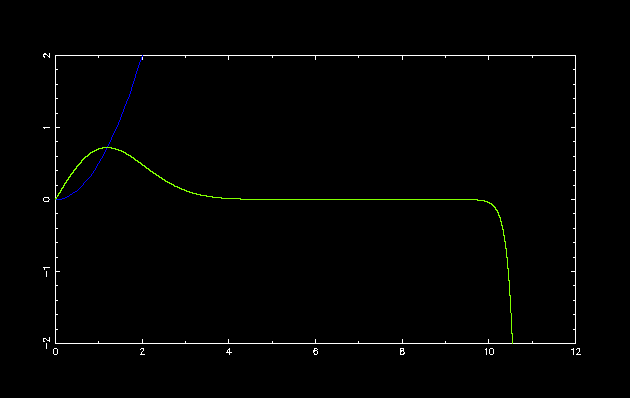
第 2 励起状態
初期設定: double E = 3.0; double dE = -1.0; int parity = 1;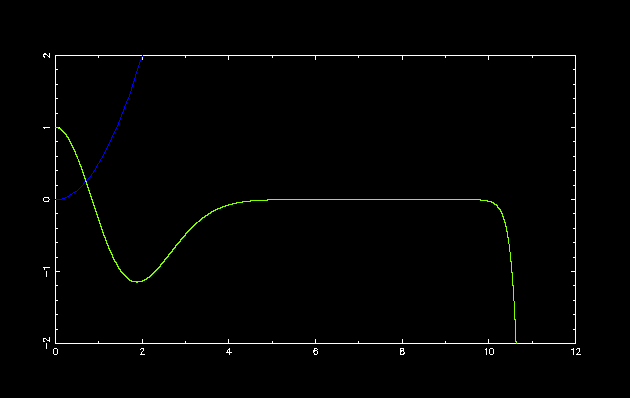
第 3 励起状態
初期設定: double E = 3.; double dE = -1.0; int parity = -1;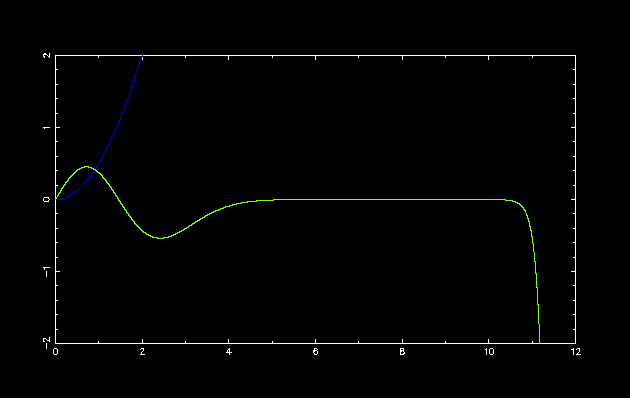
第 4 励起状態
初期設定: double E = 5.; double dE = 1.0; int parity = 1;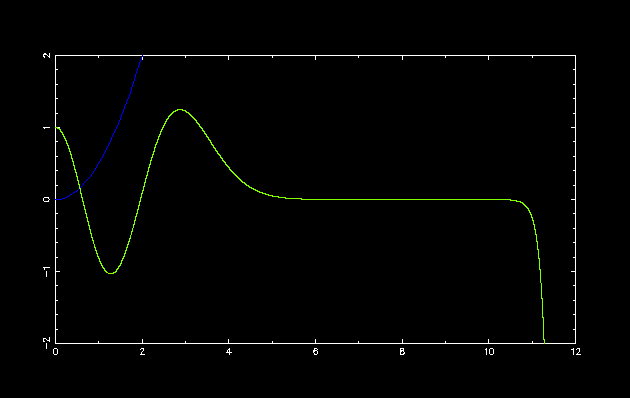
第 5 励起状態
初期設定: double E = 6.5; double dE = 1.0; int parity = -1;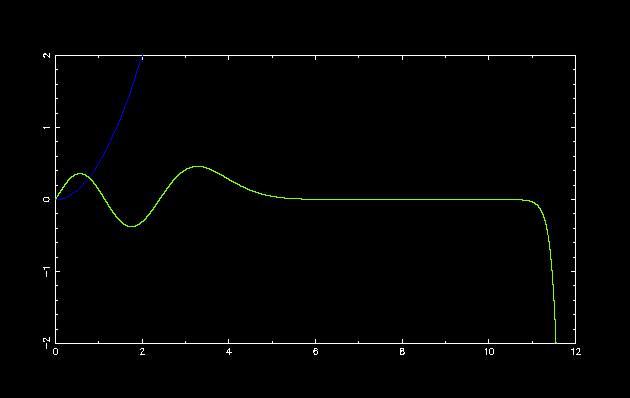
第 6 励起状態
初期設定: double E = 7.7; double dE = -1.0; int parity = 1;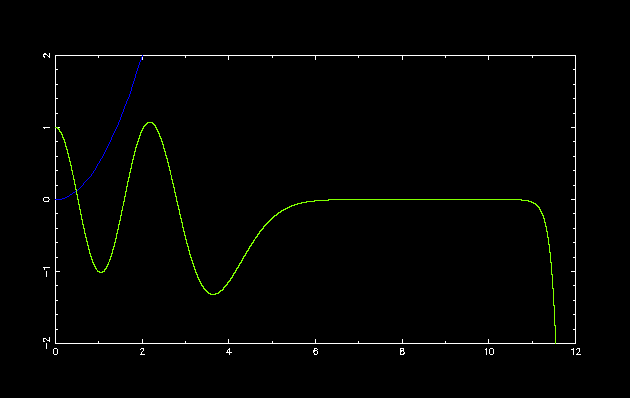
第 7 励起状態
初期設定: double E = 9.2; double dE = -1.0; int parity = -1;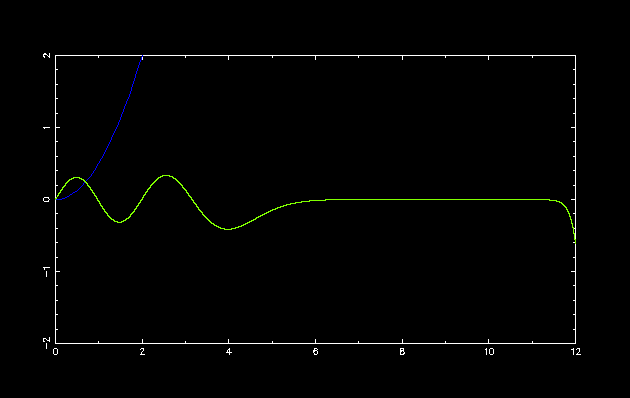
第 8 励起状態
初期設定: double E = 10.6; double dE = 1.0; int parity = 1;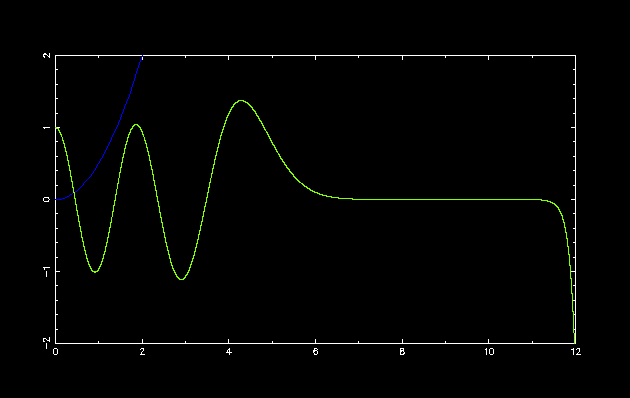
第 9 励起状態
初期設定: double E = 12.0; double dE = 1.0; int parity = -1;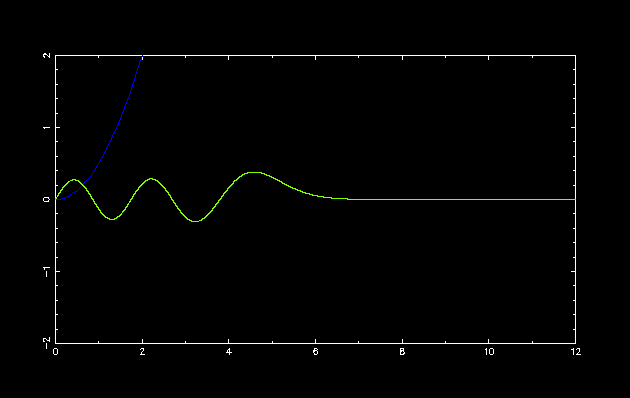
理論値との比較
数値計算で得られた固有値の値を理論値と比較します. ルンゲ・クッタ法のきざみ幅 h は 0.01 と 0.001 の二種類です.
きざみ幅 h = 0.01 の場合
| n | Eの理論値 | Eの計算値(h = 0.01) | 理論値との差 |
|---|---|---|---|
| 0 | 0.707106781186548 | 0.707106781223379 | 0.000000000036831 |
| 1 | 2.121320343559642 | 2.121320344112027 | 0.000000000552385 |
| 2 | 3.535533905932738 | 3.535533908326299 | 0.000000002393561 |
| 3 | 4.949747468305833 | 4.949747474749756 | 0.000000006443923 |
| 4 | 6.363961030678928 | 6.363961044265829 | 0.000000013586901 |
| 5 | 7.778174593052023 | 7.778174617757762 | 0.000000024705739 |
| 6 | 9.192388155425117 | 9.192388196108666 | 0.000000040683549 |
| 30 | 43.133513652379399 | 43.133517827547166 | 0.000004175167767 |
きざみ幅 h = 0.001 の場合
| n | Eの理論値 | Eの計算値(h = 0.001) | 理論値との差 |
|---|---|---|---|
| 0 | 0.707106781186548 | 0.707106781186559 | 0.000000000000011 |
| 1 | 2.121320343559642 | 2.121320343559699 | 0.000000000000024 |
| 2 | 3.535533905932738 | 3.535533905932977 | 0.000000000000239 |
| 3 | 4.949747468305833 | 4.949747468306485 | 0.000000000000652 |
| 4 | 6.363961030678928 | 6.363961030680295 | 0.000000000001367 |
| 5 | 7.778174593052023 | 7.778174593054495 | 0.000000000002472 |
| 6 | 9.192388155425117 | 9.192388155429185 | 0.000000000004068 |
| 30 | 43.133513652379399 | 43.133513652797475 | 0.000000000418076 |