一般化座標
解析力学への導入
力学の基本法則は,ニュートンの運動の法則であり,質量 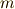 の質点が力
の質点が力 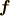 を受けたときにする運動は,
位置ベクトルを
を受けたときにする運動は,
位置ベクトルを  として具体的に次の式で表現できました.
として具体的に次の式で表現できました.

さて,式(1)はベクトルで表現されてるのでどんな座標系を選んでも成り立ちます.しかし,実際にベクトルのまま 解くことってあまりしませんよね.そこでどうするかというと,適当な座標系を選んできて成分について解くわけです.
たとえば中心力場(ひとつの大きな天体による万有引力などを思い浮かべてください)から力を受けて,質点が運動する場合を
考えて見ましょう.ポテンシャルを 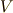 とします.このときの運動は平面上で行われることはすでに知っていることとしてお
きましょう.
とします.このときの運動は平面上で行われることはすでに知っていることとしてお
きましょう.
直交座標系 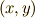 を選んだときは,式(1)は次のようにかけますね.
を選んだときは,式(1)は次のようにかけますね.
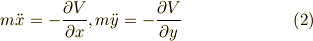
でも,中心力場の問題を解くときは極座標が便利です.そこで,極座標 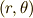 を選んで見ましょう.
式(1)は次のようになるのでしょうか??
を選んで見ましょう.
式(1)は次のようになるのでしょうか??
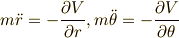
結論を言ってしまうと,このようにはできません. 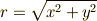 ,
,  を使って,
式(2)を変形すると次のようになります.ここは式がこの形になるということを眺めてもらうだけでかまいません.もし計算する
ときは,中心力場のポテンシャル
を使って,
式(2)を変形すると次のようになります.ここは式がこの形になるということを眺めてもらうだけでかまいません.もし計算する
ときは,中心力場のポテンシャル 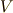 は
は  のみの関数で
のみの関数で 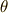 の関数ではないことに気をつけてください.
の関数ではないことに気をつけてください.
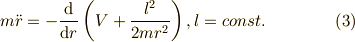
ただし, 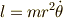 とおいています.
とおいています.
ここで注目してほしいのですが,式(2)と式(3)は同じ形にはなっていませんね.つまり,直交座標系以外で運動方程式を立てるとき は,公式を暗記するか,変数変換して直交座標系での式に代入という方法をとらないといけません.
そこで,さまざまな座標について同じ形をした運動方程式が欲しくなりますよね?そんな願いをかなえてくれるのが解析力学なのです.
では,そんな便利な解析力学に入る準備をしていきましょう!
一般化座標
運動を表現できる座標について考えてみましょう.それは,前のセクションで見たように直交座標に限りません. 極座標でも良いですし,剛体の運動なら各質点の直交座標変数より重心座標や相対座標を用いるほうが便利なときがあります. これらの新しい座標の変数について共通なことは,直交座標変数の関数として表せ,その間には1対1対応の関係が成り立っている ということです.
このような新しい座標を総称して一般化座標(もしくは一般座標)と呼ぶことにし,直交座標変数の間には1対1対応が成り立つ ことを要求しましょう.ここで注意してほしいのは,別にディメンションが同じでなくてもかまわないということです.
以下の文章で,直交座標変数は 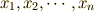 と表し,一般座標変数は
と表し,一般座標変数は 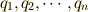 と表す
ことにします.解析力学ではたくさんの粒子を一気に扱うことが多いので,
と表す
ことにします.解析力学ではたくさんの粒子を一気に扱うことが多いので, 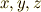 のように文字で座標を区別せずに,
添字をつけて座標を区別していきます.今のうちに慣れてしまいましょう.
のように文字で座標を区別せずに,
添字をつけて座標を区別していきます.今のうちに慣れてしまいましょう.
両変数の間には1対1対応が成立するため,両変数の関係を関数として,次のように表すことにします.より一般の
座標変換を表現できるように時間 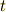 にも依存することにしましょう.
にも依存することにしましょう.
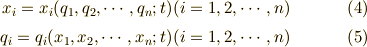
さて,上式を時間 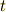 について微分してみましょう.式(4)からは,おなじみの速度
について微分してみましょう.式(4)からは,おなじみの速度 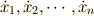 が得られますね.式(5)から得られる物理量は一般化座標の時間変化を表すものなので一般化速度
(もしくは一般速度)
が得られますね.式(5)から得られる物理量は一般化座標の時間変化を表すものなので一般化速度
(もしくは一般速度) 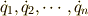 とよばれています.
チェーンルールを使って両者の関係を調べてみることにします.
とよばれています.
チェーンルールを使って両者の関係を調べてみることにします.
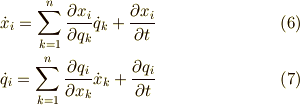
ここで 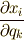 などは,一般座標の関数です.つまり,速度は一般化座標と一般化速度の関数に
なります.そのため直交座標系では座標の時間微分だけの関数だった物理量(例えば運動エネルギー)も一般座標の関数と
なるということは頭の隅にでも留めておくと今後役に立つかもしれません.
などは,一般座標の関数です.つまり,速度は一般化座標と一般化速度の関数に
なります.そのため直交座標系では座標の時間微分だけの関数だった物理量(例えば運動エネルギー)も一般座標の関数と
なるということは頭の隅にでも留めておくと今後役に立つかもしれません.
式(6)を 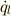 ,式(7)を
,式(7)を 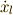 で偏微分することで次の関係式が得られます.
で偏微分することで次の関係式が得られます.
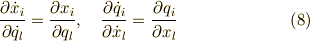
さて,これまでは座標間の関係についてみてきました.次は力についてみていきましょう.
一般化力
質点系に力が加えられている場合を考えて見ましょう.直交座標系 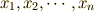 でその力は
でその力は 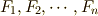 と表せたとします.このとき仮想仕事
と表せたとします.このとき仮想仕事 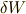 は,仮想変位
は,仮想変位 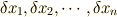 を用いて,
次のように表せますね. [*]
を用いて,
次のように表せますね. [*]
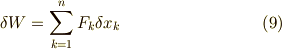
この 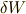 を一般化座標の仮想変位
を一般化座標の仮想変位 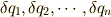 で表してみましょう.さて,
一般に
で表してみましょう.さて,
一般に 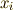 は一般化座標の関数だったので,
は一般化座標の関数だったので, 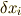 は一般化座標の仮想変位を用いた次の式で表せるはずです.(仮想変位ですから時間を動かさないことに注意してください.)
は一般化座標の仮想変位を用いた次の式で表せるはずです.(仮想変位ですから時間を動かさないことに注意してください.)
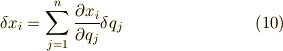
式(10)を式(9)に代入して次式を得ます.

和の順序を入れ替えて式(9)と同じ形にしてみます.
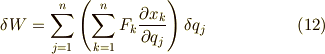
ここで, 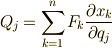 とおいて,これを
とおいて,これを 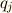 に共役な力と
定義します.
に共役な力と
定義します. 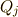 は力のディメンションを持つとは限らないため一般化力や一般力とも呼びます.これを用いれば
式(12)は式(9)とまったく同じ形で書ける事がはっきりしますね.
は力のディメンションを持つとは限らないため一般化力や一般力とも呼びます.これを用いれば
式(12)は式(9)とまったく同じ形で書ける事がはっきりしますね.
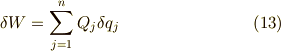
なんだか定義ばかりで疲れてしまいましたが,ようやく解析力学に入る準備が整いました. それでは次回からラグランジュの運動方程式に入っていきましょう.
| [*] | 仮想仕事や仮想変位について知らない人は, 仮想仕事の原理 をご覧ください. |