対称式への応用
ここまでの結果の応用として,対称式へガロア理論を応用することを考えてみます.この後に続く議論への準備をも兼ねています.初めて読む人は,記号が少し複雑で分かりにくいという印象を持つと思います.そういうときは,二次方程式なり三次方程式なり,簡単な例を手元で計算しつつ,記号の意味を確認するようにしてみて下さい.分かってしまえば,そんなに難しい話ではありません.
基本対称式
一般に,体 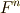 上の
上の  変数多項式は次式のように表現できます.
変数多項式は次式のように表現できます.
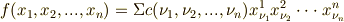
ここで係数 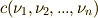 は
は 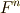 の元で,
の元で, 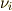 は次数(正の整数)を表すとします.ある一つの項に関して,
は次数(正の整数)を表すとします.ある一つの項に関して, 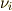 の和がその項の次数となります.いきなり一般の
の和がその項の次数となります.いきなり一般の  次の話から始めたので,少し記号がややこしく感じるかも知れませんが,
次の話から始めたので,少し記号がややこしく感じるかも知れませんが,  など,何でもいいので具体例を考えてみると記号の意味は明らかだと思います.
など,何でもいいので具体例を考えてみると記号の意味は明らかだと思います.
さて,この  変数の多項式に対し,
変数の多項式に対し,  項の置換操作
項の置換操作 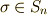 を考えます.
を考えます.
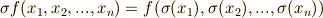
例えば,  と
と 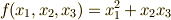 に対し,
に対し, 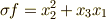 となります.この例では
となります.この例では 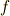 と
と 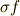 が異なる多項式となってしまいました.これに対し,
が異なる多項式となってしまいました.これに対し,  次の多項式で,
次の多項式で, 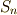 の全ての元に対して式全体が不変に保たれるものを 対称式 と呼びます.例えば,
の全ての元に対して式全体が不変に保たれるものを 対称式 と呼びます.例えば,  に対して
に対して  は対称式です.
は対称式です.
特に,基本対称式 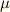 と呼ばれるものは次のように定義されます.
と呼ばれるものは次のように定義されます.

具体的に幾つか書き下してみれば,既に見慣れた形であることに気づくでしょう.
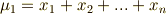
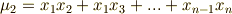

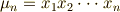
theorem
体 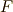 上の
上の  次対称式は,基本対称式だけを使って一意的に表現できます.
次対称式は,基本対称式だけを使って一意的に表現できます.
この定理の証明は省略します.例えば対称式 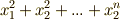 は,基本対称式を使って
は,基本対称式を使って 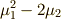 と表せます.(この例は,手を動かしてみればすぐに確認できると思います.)
と表せます.(この例は,手を動かしてみればすぐに確認できると思います.)
ガロア群と方程式の解
体 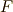 上の多項式
上の多項式 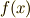 を考えます. 代数学の基本定理 によれば,
を考えます. 代数学の基本定理 によれば, 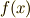 は少なくとも複素数体
は少なくとも複素数体 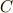 上では一次式の積に因数分解可能なはずですが,実際は
上では一次式の積に因数分解可能なはずですが,実際は 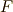 と
と 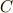 の間に無数にある中間体のどこかで,一次式の積に因数分解可能になります.そのような分解体で最小のものを, 最小分解体 と呼ぶのでした.
の間に無数にある中間体のどこかで,一次式の積に因数分解可能になります.そのような分解体で最小のものを, 最小分解体 と呼ぶのでした.
さて,ガロア拡大体について,次のような言い換えが可能でした.
Important
『  は
は 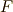 のガロア拡大体です.』⇔『
のガロア拡大体です.』⇔『  は,
は, 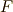 上のある分離多項式
上のある分離多項式 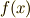 の最小分解体になっています.』
の最小分解体になっています.』
これを使って,次の定理を証明します.
theorem
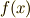 の解を
の解を 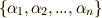 とします.ガロア群
とします.ガロア群 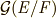 の元は,
の元は, 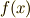 の解を置換します.
の解を置換します.
proof
ガロア群 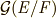 の元
の元 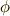 は
は 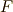 を固定体としますから,
を固定体としますから, 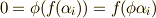 がなりたちます.よって
がなりたちます.よって  もやはり
もやはり 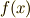 の解で,
の解で, 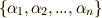 のどれか一つに等しくなります.■
のどれか一つに等しくなります.■
| [*] | 実は,ガロアが一番最初にガロア群を考えたとき,固定体や拡大体の概念から入っていったのではなく,『方程式の解を置換する操作』を考えてガロア群の考えに至ったのです.ですから,この記事では,ガロア群は方程式の解を置換するという性質を定理として紹介しましたが,当初の発見的視野に戻れば,この性質をガロア群の定義と考えても良いのでしょう.先の見通しを良くするため,対称式を復習した理由や,この辺りの事情を補足しておきます.方程式には,解と係数の関係というものがありました.二次方程式の場合は 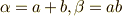 などと書けることを中学か高校で習ったと思います.解は係数の対称式によって表現されていますが,解と係数の関係は,方程式を などと書けることを中学か高校で習ったと思います.解は係数の対称式によって表現されていますが,解と係数の関係は,方程式を 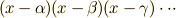 のような形に表現して展開して得られたものであることを考えれば,対称式になるのも当たり前のことです.解と係数の関係を逆に解けば,係数を解の対称式として表現することが出来ます.対称式ですから,解を置換したところで係数は不変のはずです.すなわち,係数体はこの置換に対し,固定体になっています.このような対称群を,ガロアは当初,方程式論の枠組みの中でガロア群として考えたのです.方程式が代数的に解ける条件をまだ紹介していませんので,これより先のことは説明できませんが,今までに勉強してきた,ガロア群,対称式,固定体などの概念を,この先どのように使うのかを概観しました. のような形に表現して展開して得られたものであることを考えれば,対称式になるのも当たり前のことです.解と係数の関係を逆に解けば,係数を解の対称式として表現することが出来ます.対称式ですから,解を置換したところで係数は不変のはずです.すなわち,係数体はこの置換に対し,固定体になっています.このような対称群を,ガロアは当初,方程式論の枠組みの中でガロア群として考えたのです.方程式が代数的に解ける条件をまだ紹介していませんので,これより先のことは説明できませんが,今までに勉強してきた,ガロア群,対称式,固定体などの概念を,この先どのように使うのかを概観しました. |
方程式のガロア群
体 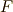 上の方程式
上の方程式  の最小分解体を
の最小分解体を  とします.このとき,
とします.このとき, 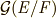 を 方程式f(x)=0のガロア群 と定義します.以後,方程式論の文脈で『方程式のガロア群』と出てきたら,係数体と最小分解体に対するガロア群だと解釈して下さい.
を 方程式f(x)=0のガロア群 と定義します.以後,方程式論の文脈で『方程式のガロア群』と出てきたら,係数体と最小分解体に対するガロア群だと解釈して下さい.
ここでもう一つ,役にたつ定理を紹介します.
theorem
既約な  次方程式
次方程式  のガロア群は,
のガロア群は,  次対称群
次対称群 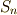 の部分群になります.
の部分群になります.
proof
既約な  次方程式
次方程式  の解を置換する
の解を置換する  次の対称群を
次の対称群を 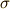 とします.ある解
とします.ある解 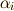 の置換
の置換 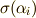 もやはり解なのですから,
もやはり解なのですから, 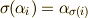 と表現してもよいはずです.実際,
と表現してもよいはずです.実際, 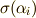 に
に 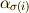 を対応させる写像は単準同型で,置換
を対応させる写像は単準同型で,置換 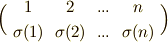 は
は 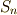 の部分群です.■
の部分群です.■
この定理の例として, 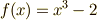 のガロア群を求めてみます.
のガロア群を求めてみます. 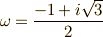 と置くと,
と置くと,  の解
の解  は次のように表わされます.
は次のように表わされます.
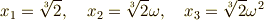
これより, 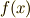 の最小分解体は
の最小分解体は 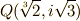 で,拡大次数は
で,拡大次数は 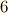 だと分かります.一般に
だと分かります.一般に 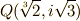 の元が,
の元が, 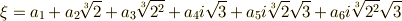 のように書けることを確認して下さい.また,ガロア群は今の定理より,
のように書けることを確認して下さい.また,ガロア群は今の定理より, 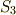 に同型です.位数
に同型です.位数  と拡大次数の関係も確認してください.
と拡大次数の関係も確認してください.
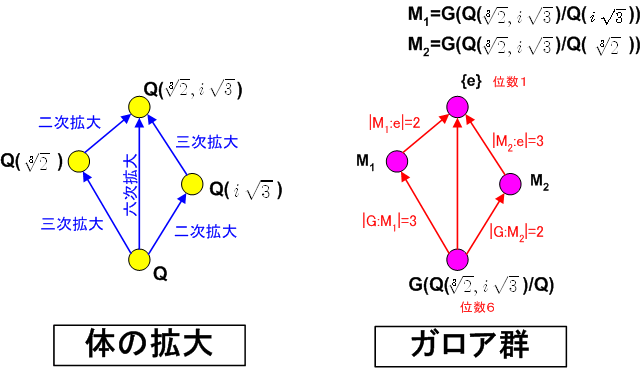
いま, 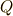 と
と 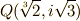 の中間体には
の中間体には 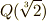 と
と 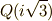 の二つが考えられます.
の二つが考えられます. ![[Q( \root 3\of {2}, i\sqrt{3}):Q( \root 3\of {2})]=3](./bbbde4c87f5e8f138c59977dac4e51b3.png) ,
, ![[Q( \root 3\of {2}, i\sqrt{3} ):Q( i\sqrt{3} )]=2](./b856801ca8a79a75ed0244d830eccdad.png) となっています.
となっています.
まず 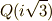 の自己同型写像として,
の自己同型写像として, 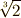 を
を 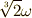 に移す写像を
に移す写像を 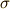 考えます.
考えます.
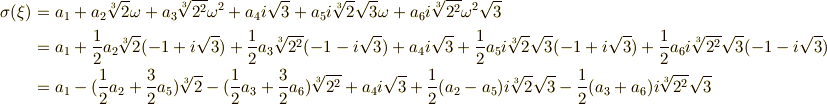
この写像は 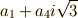 の部分を不変に保ちますので,
の部分を不変に保ちますので, 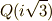 の自己同型写像であり,
の自己同型写像であり, 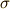 は
は 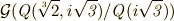 の元だと言えます.
の元だと言えます. 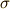 によって
によって 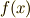 の解は
の解は  のように巡回的に置換されます.これに応じて
のように巡回的に置換されます.これに応じて 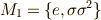 も群をなし,
も群をなし, 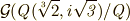 の部分群となります.
の部分群となります.
次いで 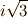 を
を  に移す写像
に移す写像  を考えます.
を考えます.  は明らかに
は明らかに 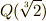 の自己同型写像で,
の自己同型写像で,  の元です.
の元です.  に注意すると,
に注意すると, 
 という群をなすことが分かります.これも
という群をなすことが分かります.これも 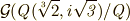 の部分群です.
の部分群です.
中間体とガロア群との対応関係を図にすると,次のようになります.拡大次数,ガロア群の位数,体とガロア群それぞれの包含関係に注意して下さい.
これらの結果と 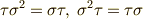 に気をつけて,
に気をつけて, 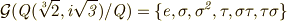 が決まります.
が決まります. 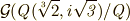 には
には 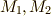 の他に,
の他に, 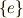 ,
, 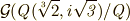 には
には 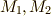 自身,そして
自身,そして 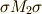 ,
, 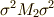 という合計六個の部分群があります.
という合計六個の部分群があります.
先ほどの中間体とガロア群の対応関係を示す図に 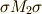 と
と 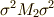 も書き込めば,さらに二本ずつ,線が増えることになります.
も書き込めば,さらに二本ずつ,線が増えることになります.