集合の元同士を足す・掛ける
この記事で勉強するのは,記号の書き方だけですので,特に難しいところは無いと思います.最後に,簡単な演習問題を載せておきます.
集合の元全てに何かを掛ける
二つの集合 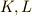 を考えます.このとき,
を考えます.このとき, 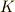 に含まれる元と,
に含まれる元と, 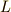 に含まれる元の積をとり,それらを全部集めた集合を
に含まれる元の積をとり,それらを全部集めた集合を  もしくは
もしくは 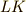 のように書きます.
のように書きます.  と
と 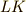 が両方あるのは,一般に積は可換ではないので,乗法の順序も重要だからです.
が両方あるのは,一般に積は可換ではないので,乗法の順序も重要だからです.
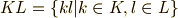
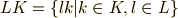
特に, 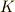 がたった一つの元
がたった一つの元  からだけなる集合
からだけなる集合 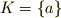 であった場合には,もう
であった場合には,もう 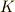 の代わりに
の代わりに  と書いてしまった方が分かりやすいですから,次のように書きます.
と書いてしまった方が分かりやすいですから,次のように書きます. 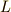 の全ての元に,左から,もしくは右から
の全ての元に,左から,もしくは右から  を掛けた集合という意味です.
を掛けた集合という意味です.
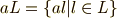
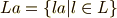
一般に, 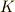 や
や 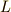 が群でも,
が群でも,  や
や 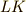 は群にならないことに注意してください.
は群にならないことに注意してください.
逆元だけ集める
次も,表記のルールです.集合 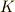 に含まれる各元に対し,その逆元だけを集めた集合を
に含まれる各元に対し,その逆元だけを集めた集合を 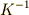 と書きます.
と書きます.
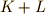 と書きます.集合同士の和集合
と書きます.集合同士の和集合 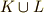 とは意味が違いますので注意してください.
とは意味が違いますので注意してください.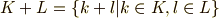
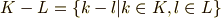
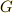 が元
が元 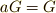
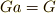
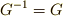
 に対し,もし
に対し,もし 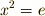 が成り立つならば,
が成り立つならば,