正多面体群3
類別とラグランジェの定理の応用を,正多面体群を使って考えてみます.最初は,正六面体群を考えます.
正六面体群
正六面体群 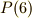 について見てみましょう.正六面体の各頂点に
について見てみましょう.正六面体の各頂点に  から
から 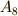 までの名前をつけることにします.正六面体群の元
までの名前をつけることにします.正六面体群の元 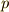 の中には,全ての頂点を置換する変換と,特定の頂点を不動に保つ変換とがあります.
の中には,全ての頂点を置換する変換と,特定の頂点を不動に保つ変換とがあります.
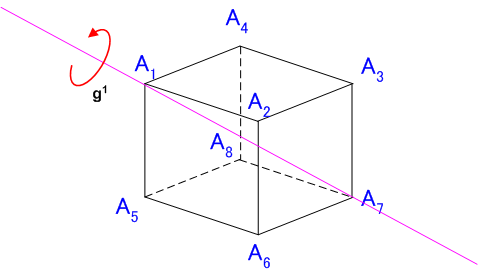
特定の頂点を不動に保つ変換とは,その頂点を通る対角線の回りに正六面体を回転させる変換です.例えば,いま仮に  を不動に保つ変換
を不動に保つ変換 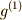 を考えると,
を考えると, 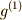 は常に
は常に 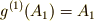 を満たすということです.変換
を満たすということです.変換 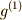 は一つではありませんが,
は一つではありませんが, 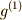 の集合は
の集合は 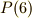 の部分群になることが示せます.
の部分群になることが示せます.
| [*] | 頂点  を不動に保つ変換の集合 を不動に保つ変換の集合 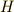 に属する二つの元 に属する二つの元 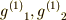 を考えるとき,これを連続的に作用させても頂点 を考えるとき,これを連続的に作用させても頂点  はやはり動きません.すなわち, はやはり動きません.すなわち, 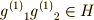 が言えて, が言えて, 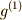 同士の積は閉じています.また 同士の積は閉じています.また 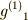 の逆元は逆回転させることですが,これが の逆元は逆回転させることですが,これが 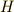 の元であることは明らかでしょう.よって の元であることは明らかでしょう.よって 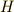 は群となり, は群となり, 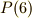 の部分群だと言えます. の部分群だと言えます. |
さて, 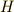 に属する変換には,恒等置換か,
に属する変換には,恒等置換か, 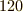 回すか,
回すか, 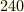 度回すか,の3種類しかありませんでしたので,
度回すか,の3種類しかありませんでしたので, 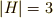 が言えます.この
が言えます.この 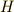 を使って,
を使って, 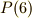 を類別しましょう.
を類別しましょう. 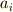 を,頂点
を,頂点  を頂点
を頂点 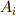 へ移す変換だとすると,
へ移す変換だとすると, 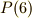 は次のように類別できます.
は次のように類別できます.
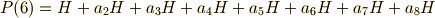
従って, 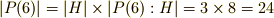 が分かります.
が分かります.
その他の正多面体群
他の正多面体群も,同様の手法で位数を求められることを見ましょう.
| 頂点の数 | その頂点を不動に保つ変換の数 | 群の位数 | |
|---|---|---|---|
| 正四面体 | 4 | 3 | 12 |
| 正六面体 | 8 | 3 | 24 |
| 正八面体 | 6 | 4 | 24 |
| 正十二面体 | 20 | 3 | 60 |
| 正二十面体 | 12 | 5 | 60 |
ある頂点に対し,その頂点を不動に保つ変換の数( 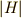 )は,その頂点に集まる辺の数と同じです.正六面体に対しては,対称群と対応させることですぐに解く方法が簡単でしたが( 正六面体群 を参照),正二十面体のように複雑なものには,視覚的に対称群を対応させるのは困難でした.ここで紹介した,剰余類分解を使う方法ならば,正二十面体でも一つの頂点だけに着目すれば良いので,視覚的にも簡単に計算できます.表中の頂点の数が
)は,その頂点に集まる辺の数と同じです.正六面体に対しては,対称群と対応させることですぐに解く方法が簡単でしたが( 正六面体群 を参照),正二十面体のように複雑なものには,視覚的に対称群を対応させるのは困難でした.ここで紹介した,剰余類分解を使う方法ならば,正二十面体でも一つの頂点だけに着目すれば良いので,視覚的にも簡単に計算できます.表中の頂点の数が 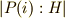 にあたります.
にあたります.
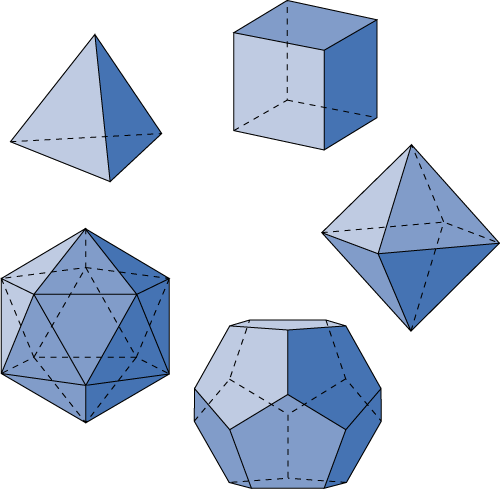
いろいろな見方があるもんですね!