三次方程式
ガロア理論を使って方程式の可解性を考える例として,二次方程式に引き続き, 三次方程式を考えてみます.二次方程式よりもずっと複雑になりますから,頑張りましょう.中間体も出てきます.
三次方程式
次の形の三次方程式を基本形として考えます.
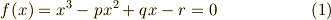
ここで係数 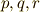 は体
は体 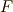 の元とします.また,
の元とします.また, 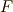 は
は  の立方根を含むものとします.
の立方根を含むものとします.
| [*] |  の立方根は の立方根は 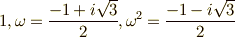 の三つだけですが, の三つだけですが, 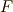 が例え が例え  の立方根を含まないとしても, の立方根を含まないとしても, 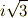 さえ添加すれば,全ての立方根を含む体を作れます.そんな体を さえ添加すれば,全ての立方根を含む体を作れます.そんな体を 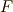 だと考えても一般性を失いませんから,都合よく,最初から だと考えても一般性を失いませんから,都合よく,最初から 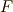 は は  の立方根を含むものとします. の立方根を含むものとします. |
また, 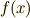 の最小分解体を
の最小分解体を 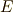 とします.ガロア群
とします.ガロア群 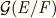 は,
は, 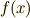 の解
の解 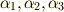 を並べ替える 対称群 です.もしも,
を並べ替える 対称群 です.もしも, 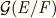 が,全ての並べ替えを含むとすると,つまり
が,全ての並べ替えを含むとすると,つまり 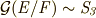 とすると,
とすると, 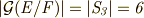 となるはずです.ここで,
となるはずです.ここで, 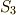 は次のような 正規部分群の組成列 を持つことを思い出しましょう.
は次のような 正規部分群の組成列 を持つことを思い出しましょう.

| [†] | 重解を持つなど,方程式によってはガロア群が 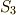 より小さくなる場合があるかも知れませんが,一番一般的な場合として, より小さくなる場合があるかも知れませんが,一番一般的な場合として, 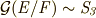 を考えています. を考えています. |
交代群 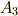 の位数は
の位数は 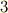 で, 商群
で, 商群 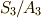 の位数は
の位数は 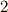 と分かります.位数
と分かります.位数 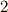 の群は全て可換群ですから,
の群は全て可換群ですから, 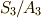 は可換群です.また,
は可換群です.また, 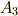 も可換群です.これより
も可換群です.これより 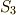 は可解群だということが分かります.さて,
は可解群だということが分かります.さて, 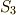 の部分群
の部分群 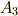 によって不動に保たれる中間体
によって不動に保たれる中間体 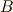 を考えてみましょう.( 交代群 とは,対称群の中の偶置換だけによる部分群です.可解群の定義については, こちら を参照して下さい.)
を考えてみましょう.( 交代群 とは,対称群の中の偶置換だけによる部分群です.可解群の定義については, こちら を参照して下さい.)

ガロア群に正規部分群があり,それに対応して拡大体の昇鎖列に中間体を一つ考えなければならない分だけ, 二次方程式 のときよりも議論がずっと複雑になっていることに注意しましょう. 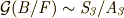 より
より ![[B:F]=2](./d558fbcc3aca7faba92a9515e673b72d.png) で,
で, 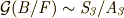 が可換群であるのは明らかですから,
が可換群であるのは明らかですから, 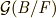 は可解群となります.この段階で,三次方程式は代数的に解けると判断できます.(
は可解群となります.この段階で,三次方程式は代数的に解けると判断できます.(  も確認して下さい.)さて,
も確認して下さい.)さて, 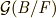 の元は
の元は 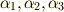 の偶置換の全体ですから,次式で定義される
の偶置換の全体ですから,次式で定義される 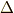 は,明らかに
は,明らかに 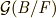 の元によって不動に保たれ,
の元によって不動に保たれ, 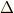 は
は 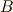 の元だと言えます.(一般に,
の元だと言えます.(一般に, 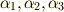 の置換によって
の置換によって 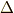 は
は 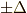 に移されますが,偶置換では
に移されますが,偶置換では 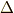 は
は 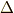 にしか移されないことに注意!)
にしか移されないことに注意!)
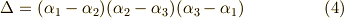
また, ![[B:F]=2](./d558fbcc3aca7faba92a9515e673b72d.png) を思い出せば,
を思い出せば, 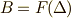 が言えます.ここで,ラグランジェのリゾルベントを考えてみましょう.
が言えます.ここで,ラグランジェのリゾルベントを考えてみましょう.
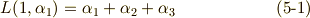
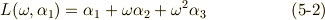

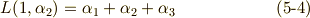
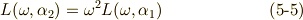
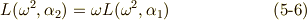
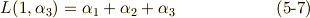
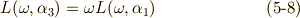
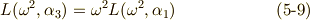
三次方程式の解は, 累開冪拡大体とガロア群の関係 の式 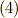 で定義したように,これらのラグランジェのリゾルベントを足し合わせて
で定義したように,これらのラグランジェのリゾルベントを足し合わせて 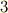 で割ったものになります.
で割ったものになります.
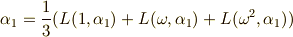
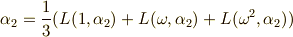

ただし,これではまだ式 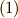 の係数だけを使った表現になっていませんし,
の係数だけを使った表現になっていませんし, 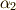 や
や 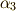 も示さないといけません.この後の計算はかなり面倒ですが,ラグランジェのリゾルベントの各項を
も示さないといけません.この後の計算はかなり面倒ですが,ラグランジェのリゾルベントの各項を 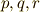 と
と  の立方根
の立方根 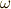 (つまり
(つまり 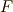 の元だけ)で表わす努力をします.(このことが可能なことは, 累開冪拡大体とガロア群の関係 で証明していますので,あとはやっつけ仕事です.)
の元だけ)で表わす努力をします.(このことが可能なことは, 累開冪拡大体とガロア群の関係 で証明していますので,あとはやっつけ仕事です.)
まず,解と係数の関係が使えそうです.

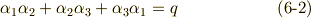

また,先ほど定義した 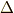 は,
は, 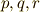 を使って次のように表現できます.(この計算は面倒ですが,代入すれば確認できますので,導出は省略します.)
を使って次のように表現できます.(この計算は面倒ですが,代入すれば確認できますので,導出は省略します.)

さらに, 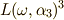 と
と 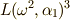 は,次のように
は,次のように  だけで表現できることが分かります.(この計算はもっと面倒なので,導出は省略します. 累開冪拡大体とガロア群の関係 で示したように,
だけで表現できることが分かります.(この計算はもっと面倒なので,導出は省略します. 累開冪拡大体とガロア群の関係 で示したように, 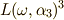 と
と 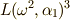 は
は 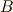 の元であることを確認して下さい.)
の元であることを確認して下さい.)
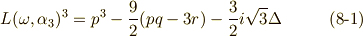
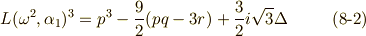
式  と式
と式 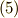 を見比べれば,
を見比べれば, 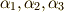 を
を 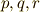 と
と 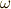 だけで表わす道筋が見えるのではないでしょうか.
だけで表わす道筋が見えるのではないでしょうか. 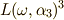 の立方根の一つを
の立方根の一つを 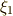 とします.
とします.

また, 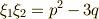 を満たすように,
を満たすように, 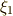 から
から 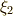 を決めます.この
を決めます.この 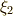 が
が 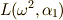 になります.(これは式
になります.(これは式 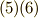 から示せます.)この
から示せます.)この 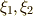 を使うと,ラグランジェのリゾルベントを,次のように書き直せます.
を使うと,ラグランジェのリゾルベントを,次のように書き直せます.
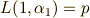

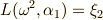
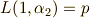
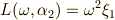
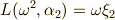
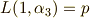
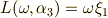

よって,式 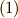 の解は次のように表わせます.
の解は次のように表わせます.

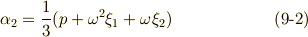

| [‡] | 特に, 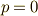 の場合, カルダノの公式 に帰着することを確かめてみて下さい. の場合, カルダノの公式 に帰着することを確かめてみて下さい. 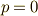 の形(三次方程式の標準形)に帰着させることはいつでも可能ですが,式 の形(三次方程式の標準形)に帰着させることはいつでも可能ですが,式 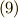 を見れば, を見れば, 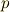 が零でない形も一般解を示されていることが分かります. が零でない形も一般解を示されていることが分かります. |
