交換子群
五次方程式の可解性に関して,交換子群の定理を使いたいので,ここで交換子群という群を紹介します.この記事は補足的なもので,ガロア理論の大筋とは,あまり関係がありません.交換子群について知りたくて,いきなりこの記事を読んでいる人は,ガロア理論に関する説明は無視して読んで下さい.
交換子群
群 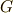 の元
の元 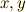 に対し,
に対し, 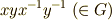 を,元
を,元 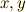 の 交換子 もしくは 交換子積 と呼びます.そして,交換子によって生成される群を 交換子群 と呼びます.交換子群は単位元
の 交換子 もしくは 交換子積 と呼びます.そして,交換子によって生成される群を 交換子群 と呼びます.交換子群は単位元 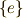 だけの最小のものから,群
だけの最小のものから,群 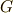 自身になる場合もあります.交換子を
自身になる場合もあります.交換子を ![[x,y]](./8ca042e8ff30aba99a78e069db08b58a.png) と表わし,群
と表わし,群 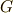 の交換子群を
の交換子群を 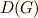 と表わします.(
と表わします.( 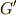 と表わしている本もありますが,ここでは
と表わしている本もありますが,ここでは 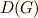 を採用します.)まずは,交換子群がたしかに群になることを見てみましょう.
を採用します.)まずは,交換子群がたしかに群になることを見てみましょう.
- 交換子を取る操作に対して,交換子群は閉じています.(
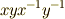 と
と 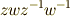 の交換子積
の交換子積 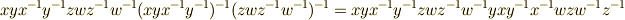 で,
で, 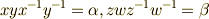 と置けば,
と置けば, 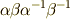 と書けて,確かに交換子群に含まれることが分かります.)
と書けて,確かに交換子群に含まれることが分かります.) - 任意の元
 と
と  との交換子積は
との交換子積は  になりますので,
になりますので,  交換子群に含まれ,交換子積の単位元だと言えます.
交換子群に含まれ,交換子積の単位元だと言えます. 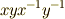 の逆元は
の逆元は 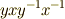 ですが,これも確かに交換子群の元です.
ですが,これも確かに交換子群の元です.
また, 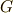 の元の積に関して結合則はなりたつはずなので,
の元の積に関して結合則はなりたつはずなので, 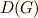 の元の交換子積でも結合則がなりたつことは明らかです.
の元の交換子積でも結合則がなりたつことは明らかです.
次に,交換子群に関して,いくつか重要な定理を紹介します.(これらは,ガロア理論の証明で使うので,いまここで何の役に立つのかよく分からなくても,気にしないで下さい.)
theorem
群 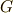 が可換群であることと,
が可換群であることと, 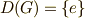 となることは同値です.
となることは同値です.
proof
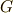 が可換群なら,任意の元
が可換群なら,任意の元 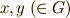 に対して
に対して 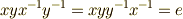 となります.■
となります.■
この定理の証明は簡単すぎでしたが,結果は大事です.
theorem
群 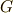 の交換子群
の交換子群 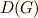 は
は 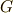 の正規部分群で,商群
の正規部分群で,商群 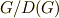 は可換群になります.
は可換群になります.
proof
群 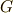 の任意の元
の任意の元  に対して,
に対して,  と書けますので,
と書けますので, 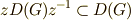 が言えます.これより
が言えます.これより 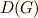 が正規部分群であることが分かりました.■
が正規部分群であることが分かりました.■
theorem
群 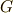 の正規部分群
の正規部分群 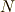 に対して,商群
に対して,商群 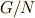 が可換群となることは,
が可換群となることは, 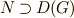 となることと同値です.
となることと同値です.
proof
まず 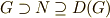 とすると,
とすると, 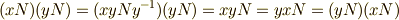 が成り立つので,商群
が成り立つので,商群 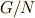 は可換群だということが言えます.( 商群
は可換群だということが言えます.( 商群 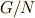 の単位元は
の単位元は 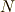 ,
, 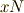 の逆元は
の逆元は 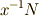 であることを思い出してください.)逆に,
であることを思い出してください.)逆に, 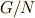 が可換群であれば,任意の元
が可換群であれば,任意の元 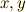 に対して
に対して 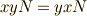 より
より 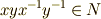 ,すなわち
,すなわち 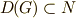 が示せます.■
が示せます.■
立て続けに定理を紹介してしまいましたが,証明は簡単だったので大丈夫だと思います.少し混乱してしまった人も,定理を使うときに再び戻って来れば,大丈夫だと思います.次の定理が,ガロア理論で本質的に重要です.実は,あとでこの定理を使いたくて,ここに交換子群の記事を挿んだのでした.
theorem
五次以上の交代群 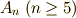 では,
では, 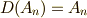 となります.
となります.
proof
五次以上の対称群 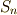 を考えてみます.最低,五次の置換を考えることができるので,
を考えてみます.最低,五次の置換を考えることができるので, 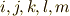 の五文字を考えると,常に
の五文字を考えると,常に 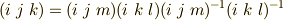 が成り立ちますので,三次の置換全体は
が成り立ちますので,三次の置換全体は 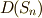 になることが分かります.一方,交代群は偶置換の集まりでしたが,三次以上の偶置換は全て三次の巡回置換の積として表現できるということでしたので( 対称群2 参照),
になることが分かります.一方,交代群は偶置換の集まりでしたが,三次以上の偶置換は全て三次の巡回置換の積として表現できるということでしたので( 対称群2 参照), 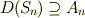 が言えます
が言えます 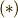 .また,商群
.また,商群 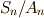 は位数
は位数 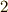 なので可換群ですが,先ほど示した定理によって,
なので可換群ですが,先ほど示した定理によって, 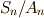 が可換群になることは,
が可換群になることは, 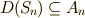 となることと同値です
となることと同値です 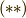 .
. 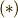 と
と 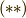 より,一般に
より,一般に 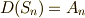 が分かります.特に
が分かります.特に 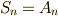 と置けば,
と置けば, 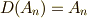 が示されます.■
が示されます.■
交換子群の交換子群,つまり 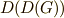 を
を 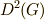 のように書くことがあります.交換子群は正規部分群になるのですから,
のように書くことがあります.交換子群は正規部分群になるのですから, 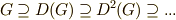 となるはずで,
となるはずで, 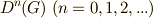 の並びは,
の並びは, 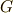 の正規部分群の組成列(かその一部)になるはずです.こんな話題があったことも,頭の片隅に引っ掛けておいて下さい.
の正規部分群の組成列(かその一部)になるはずです.こんな話題があったことも,頭の片隅に引っ掛けておいて下さい.