代数方程式の性質
この辺りで代数方程式の基本的な性質を復習しておきます.主なトピックは,中学校や高校で習う因数分解や剰余定理などです.体の概念が新しいかも知れませんが,それ以外に難しい話はないと思います.
代数方程式の定義
(このセクションは 代数学の基本定理 に載せた定義を再掲します.)
有限個の数や文字を,『 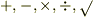 』の5つの演算だけを組み合わせて作った式を 代数式 と呼びます.(それに対して,
』の5つの演算だけを組み合わせて作った式を 代数式 と呼びます.(それに対して,  や
や 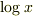 の入っている式を 超越式 と呼びます).
の入っている式を 超越式 と呼びます).
未知数が代数式の形で表される方程式を 代数方程式 と呼びます.これは既にみなさんのよく知っている次の形の方程式です.
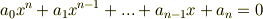
| [*] | 左辺の部分を 多項式 と呼びます.方程式を解くとは,多項式 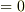 を満たす変数(多項式の 零解 と呼びます)を見つけることと見ても良いわけです.今後,上式の左辺だけを指す場合に多項式,多項式の零解を見つけることを念頭に置いている場合には方程式と呼ぶようにしますが,方程式を解くことを多項式を解くと言ってしまう人もいます.しかし,意図する意味は明快ですし,それで混乱して困るようなこともありませんので,それほどこの用語に神経質になる必要はないと思います. を満たす変数(多項式の 零解 と呼びます)を見つけることと見ても良いわけです.今後,上式の左辺だけを指す場合に多項式,多項式の零解を見つけることを念頭に置いている場合には方程式と呼ぶようにしますが,方程式を解くことを多項式を解くと言ってしまう人もいます.しかし,意図する意味は明快ですし,それで混乱して困るようなこともありませんので,それほどこの用語に神経質になる必要はないと思います. |
体と多項式
すでに 体に関する基本的なこと で触れましたが,代数方程式を解く(多項式 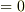 を満たす解を見つける)ことは,体論抜きには考えられません.多項式の係数が体
を満たす解を見つける)ことは,体論抜きには考えられません.多項式の係数が体 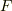 に含まれる数であるとき,これを『
に含まれる数であるとき,これを『 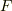 上の多項式』と呼びます.
上の多項式』と呼びます.
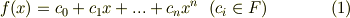
ここで  の最高次数(この場合
の最高次数(この場合  )をこの多項式の 次数 と呼び,
)をこの多項式の 次数 と呼び, 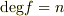 のように書きます.最高次の項の係数(この場合
のように書きます.最高次の項の係数(この場合  )を 主係数 と呼びます.二つの多項式を足したり掛けたりしたとき,次数に関して次の関係が成り立ちます.
)を 主係数 と呼びます.二つの多項式を足したり掛けたりしたとき,次数に関して次の関係が成り立ちます.
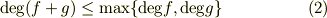

この関係は,ちょっと例を考えてみればすぐに分かることなので,証明は省略します.定数関数 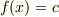 の次数は
の次数は 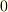 です.
です. 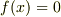 には次数を定めません.
には次数を定めません.
| [†] | 方程式の係数体に応じて『〜上の多項式』と呼ぶということでしたが,解  がどのような体に属する数なのかは,これだけでは何とも言えません.有理係数の方程式を解いて複素数解が出てくることもあるわけですから, がどのような体に属する数なのかは,これだけでは何とも言えません.有理係数の方程式を解いて複素数解が出てくることもあるわけですから,  は体 は体 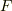 の範囲を『はみ出す』可能性が多いにあります.むしろ,解は係数体をはみ出るのが普通でしょう.今後,解を含む体に関して色々なことを考えていきます. の範囲を『はみ出す』可能性が多いにあります.むしろ,解は係数体をはみ出るのが普通でしょう.今後,解を含む体に関して色々なことを考えていきます. |
商の定理と剰余定理
多項式を多項式で割る,という操作を定義できます.多項式 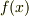 を,それより次数の低い多項式
を,それより次数の低い多項式 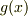 を使って,次のように表現できます.
を使って,次のように表現できます.
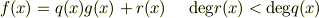
ここで 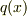 を商,
を商, 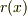 を剰余と呼びます.
を剰余と呼びます. 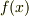 が
が 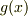 で割り切れない場合,剰余の次数は商の次数より小さくなります.例えば,
で割り切れない場合,剰余の次数は商の次数より小さくなります.例えば, 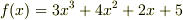 を
を 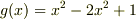 で割ると次のように書けます.
で割ると次のように書けます.
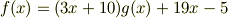
こんな計算練習問題を,中学校や高校でやったことがあると思います. 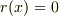 のとき,
のとき, 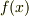 は
は 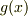 で割り切れると言います.
で割り切れると言います.
剰余定理
特に 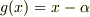 の形のとき,
の形のとき, 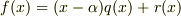 と書けますが,
と書けますが, 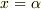 を代入すると
を代入すると 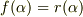 となりますので,剰余の部分を次のように書き換えられます.
となりますので,剰余の部分を次のように書き換えられます.
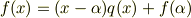
これを 剰余定理 と呼びます.
方程式の解
体 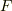 上の点
上の点  が
が 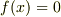 の解であるとは,
の解であるとは,  が
が  を満たすことです.剰余定理を使えば,
を満たすことです.剰余定理を使えば,  が
が 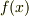 を割り切ることであると言い換えても良いでしょう.
を割り切ることであると言い換えても良いでしょう.
ここで,次の定理がなりたちます.
theorem
体 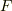 上の
上の  次方程式は,
次方程式は, 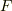 上に高々
上に高々  個の解を持ちます.
個の解を持ちます.
proof
帰納法によって証明します.まず次数が零の方程式,つまり  は,
は,  の方程式になっていませんから,
の方程式になっていませんから, 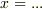 の形の解はありません.
の形の解はありません. 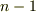 次方程式に対して仮定が正しく, 高々
次方程式に対して仮定が正しく, 高々 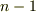 個の解が存在するとします.このとき
個の解が存在するとします.このとき  次方程式
次方程式 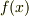 を考えてみます.解が無ければ、議論はここで終わりですが,仮定には矛盾しません.また,少なくとも1つは解
を考えてみます.解が無ければ、議論はここで終わりですが,仮定には矛盾しません.また,少なくとも1つは解  を持つとすれば,
を持つとすれば, 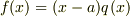 (
( 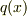 は
は 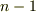 次多項式)と書けて,仮定より
次多項式)と書けて,仮定より 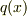 は高々
は高々 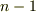 個の解を持ちますので定理が示されます.■
個の解を持ちますので定理が示されます.■
解の個数は 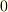 〜
〜  のいずれかで,それは係数の属する体によるわけですが,体が複素数体の場合に限って,
のいずれかで,それは係数の属する体によるわけですが,体が複素数体の場合に限って,  次方程式は常に
次方程式は常に  個の解を含むことが知られています.これは,『代数学の基本定理』の名で知られている大変有名かつ重要な定理です.
個の解を含むことが知られています.これは,『代数学の基本定理』の名で知られている大変有名かつ重要な定理です.
theorem
複素数体C上のn次方程式は,C上にn個の解を持つ.
この定理の証明は,体論の他に複素積分の知識を必要とするのでここでは示しません.(歴史的背景については 代数学の基本定理 を参照してください.) しかし,この定理の結果は今後とも非常に大事なので,とりあえず結果だけを認めて先へ進むことにします.
既述した内容の繰り返しになりますが,ここで勉強した要点をおさらいしておきましょう.ある体 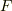 上の
上の  次代数方程式は,
次代数方程式は, 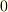 〜
〜  個の解を持ちます.
個の解を持ちます. 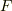 上の解が
上の解が  以下の場合には,残りの解が,
以下の場合には,残りの解が, 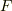 からはみ出てしまっているわけです.考える体を少し拡大すれば,もう少したくさん解が見つかるでしょう.そして,複素数体にまで拡大すれば,
からはみ出てしまっているわけです.考える体を少し拡大すれば,もう少したくさん解が見つかるでしょう.そして,複素数体にまで拡大すれば,  個の解全てが見つかるということです.方程式の解の有無を,拡大体の考えを使って考えると,そのような仕組みが見えてきます.
個の解全てが見つかるということです.方程式の解の有無を,拡大体の考えを使って考えると,そのような仕組みが見えてきます.
因数分解
体 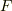 上の
上の  次方程式
次方程式 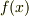 が
が 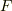 上に
上に  個全ての解を持つとき,
個全ての解を持つとき, 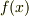 は『
は『 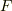 上で因数分解可能である』と言われます.このとき,解
上で因数分解可能である』と言われます.このとき,解 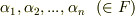 を使って
を使って 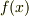 を次のように 一次式の積の形に式変形できます .
を次のように 一次式の積の形に式変形できます .
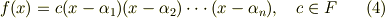
代数学の基本定理に従えば,このような式変形は複素数体 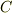 上では常に保証されますが,その他の体上の方程式では『
上では常に保証されますが,その他の体上の方程式では『 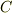 には含まれるけれども
には含まれるけれども 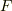 からははみ出る』という解が幾つか存在する可能性があるため,一次式の積に因数分解できるとは限りません.
からははみ出る』という解が幾つか存在する可能性があるため,一次式の積に因数分解できるとは限りません.
また,式 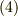 は
は 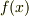 の解を明示的に示す形であり,最終的にこのように変形できれば,方程式の解が一目瞭然に分かります.代数学の基本定理は,どんな方程式でも複素数体上で考えれば,この形に書けることを保証しています.ところが『与えられた方程式を,どうやって式
の解を明示的に示す形であり,最終的にこのように変形できれば,方程式の解が一目瞭然に分かります.代数学の基本定理は,どんな方程式でも複素数体上で考えれば,この形に書けることを保証しています.ところが『与えられた方程式を,どうやって式 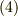 の形に変形したらいいのか?』という肝心の部分の情報が一切不明です.つまり, 代数学の基本定理は,ある代数方程式が『解ける』かどうかを保証するものではありません.解の存在を保証するだけです.
の形に変形したらいいのか?』という肝心の部分の情報が一切不明です.つまり, 代数学の基本定理は,ある代数方程式が『解ける』かどうかを保証するものではありません.解の存在を保証するだけです.
加・減・乗・除・開冪(  乗根を求めること)の5つの方法を,有限回だけ繰り返して与えられた方程式を式
乗根を求めること)の5つの方法を,有限回だけ繰り返して与えられた方程式を式 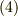 の形に変形することを『方程式を代数的に解く』と言いますが,与えられた方程式が代数的に解けるかどうかはまた別の問題であり,ガロア理論で論じられることになります.
の形に変形することを『方程式を代数的に解く』と言いますが,与えられた方程式が代数的に解けるかどうかはまた別の問題であり,ガロア理論で論じられることになります.
いま勉強したばかりの拡大体の考えを使うと,『体 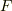 上の方程式
上の方程式 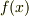 が解けるかどうか』という問題と,『
が解けるかどうか』という問題と,『 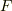 と
と 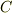 の間のどこかにある,
の間のどこかにある, 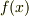 の解を全て含む体に
の解を全て含む体に 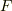 を上手に拡大できるか』という問題が同値だということが分かるでしょう.
を上手に拡大できるか』という問題が同値だということが分かるでしょう.