波の大事な性質
ここでは,波というものを表す量と,それらの間にある重要な関係を見て行きます.
波の基本量
波を表す基本的な量として,速さ,振幅,波長,振動数があります.
下の絵をみてください.
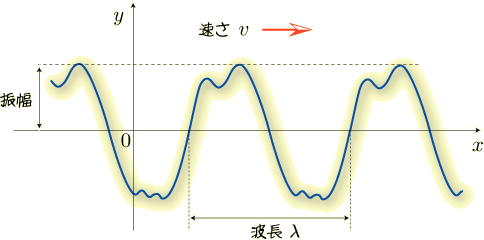
波っていうとだいたいこんなもんですよね.クネクネうねってる.
一定の間隔で同じ形を繰り返しているものが,波です [*] .
波は水面をみればすぐにみつかるので,イメージしやすいでしょう.
これはその断面図だと思ってください.
実際みるのは3次元ですが,この図では  と
と 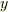 の2次元にしてあります.
の2次元にしてあります.  が距離,
が距離, 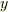 が高さです.
が高さです.
波とはどういうものか考えてみると,池に石を投げたり海をみれば分かるように「動くもの」です [†] . しかし,たとえばボールが飛んでいったりするのとはちょっと違います. 遠くの波がこちらへ押し寄せて来ても,遠くの物質が実際にこちらへ来るのではありません. 水面(もちろん水じゃなくてもいい)を伝わって来るものが波といえるでしょう. そして波が伝わったかどうかは,水面が上下することで分かります.
| [*] | 正確なことを言い出すと「空間や物体内のある部分での振動や変化が次々に隣りの部分に有限の速度で伝わり,遠くまで及んでいく現象を波または波動という」( 三省堂物理小事典 第4版)と記載があります.だけどこの記事では単純に“同じ形が繰り返し現れているもの”を波と呼んでおきます. |
| [†] | これまた正確には,動かない波も存在します.この記事で扱うような動いている波を「進行波」と呼び,動かない波を「定常波」または「定在波」と呼んで区別することもあります. |
波長 λ [m]
文字どおり波の長さですが,どこからどこを波の長さとするのかが注意点です. 上の図のように横軸に距離,縦軸に変位(高さ)のグラフを書くと,同じ形が繰り返し繰り返し現れているのが見て取れます. その波の形ひとつ分の長さを,1波長といいます.
長さの測り初めの位置はどこにしても,波長は変化しません.横軸との交点などのように,わかりやすい場所を目印にしましょう.
波長はふつう 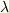 (ラムダ)という記号で表します.単位は
(ラムダ)という記号で表します.単位は 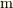 (メートル)です.
(メートル)です.
振幅 A [m]
波がどれくらい振れているかを表すのが振幅です.
縦軸を高さとしてグラフを書いたとき,グラフの一番下と一番上を比較して,高さの違いを振動の幅と呼んだりします. その振動の幅の半分の長さを,振幅といいます.
記号は特に決まってないようですが, 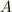 で表すことが多いように思います.
単位は波長と同じく
で表すことが多いように思います.
単位は波長と同じく 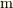 です.
です.
速さ v [m/s]
波はふつうじっとしておらず,時間とともに動きます.
だから「速さ」があります.単位はおなじみの 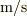 (メートル毎秒)です.
(メートル毎秒)です.
振動数 f [Hz]
1秒間に何回振動しているか…という回数を,振動数と呼びます.
では振動の回数をどのように数えるのか?ってことを説明していきましょう.
波は時間とともに動くといっても,ある場所の水面だけじっと注目していると,水面は上下に水位を変化させているだけです.
次の絵を見てみてください.
まず,時刻 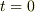 のとき下のような波だったとします.原点の赤丸に注目してください.
のとき下のような波だったとします.原点の赤丸に注目してください.
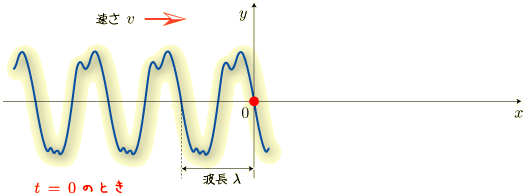
少し時間が経って波が動くと,原点での水位は上昇します.
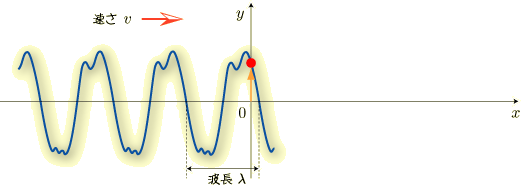
もう少し経つと今度は下がります.
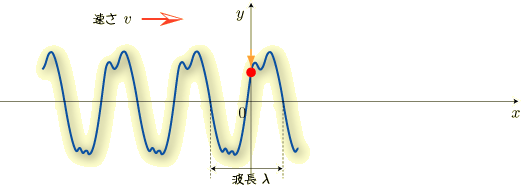
さらに下がったあと,
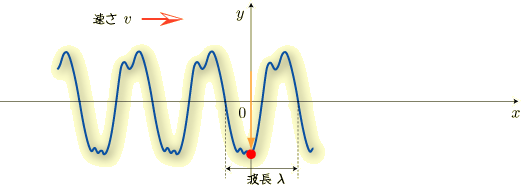
今度は上昇して元の位置の戻ります. これで1回振動したことになります.
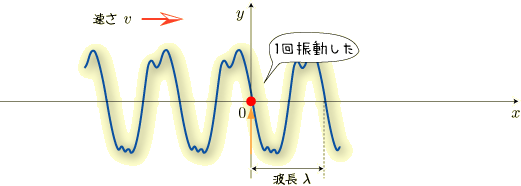
最初と同じ形を描き始めるまでを,1回の振動と数えるわけです.
ここまででちょうど1秒間だったら振動数は1ということになります.
0.5 秒だったら振動数は 2,3 秒だったら振動数は 0.333 ... ということになります.
1 秒あたり何回振動するかなので,単位は 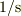 (毎秒)ですが,
ふつうこれを
(毎秒)ですが,
ふつうこれを 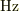 (ヘルツ)といいます.
家電製品だと振動数ではなく「周波数」と呼ばれていることが多いですが,同じ意味です.
(ヘルツ)といいます.
家電製品だと振動数ではなく「周波数」と呼ばれていることが多いですが,同じ意味です.
また,振動数の逆数で「1回振動するのに何秒かかるか」という量が周期です.この単位は  (秒)です.
(秒)です.
波の重要な関係式
最後に,波の重要な関係式を覚えてもらいます.この関係は普遍的なもので,いつも成り立ちます. 波が出てくると必ずといっていいほど出てくる関係で,量子力学でももちろん登場します.それは
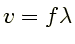
という関係です.ブイいこーるエフらむだ.いま振動数のところで波が進む様子をみてきました.
その続きで,時刻 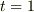 のときにしたのような状態になったとします.
のときにしたのような状態になったとします.
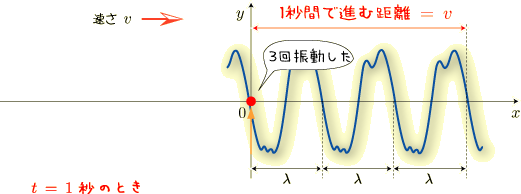
このとき波の進んだ距離は,ちょうど 1 秒間ですから速度  です(速度とは 1 秒間に進む距離のこと!).
そして波は 3 波長分進み,3 回振動していますから振動数は 3 です.
です(速度とは 1 秒間に進む距離のこと!).
そして波は 3 波長分進み,3 回振動していますから振動数は 3 です.
 の長さは波 3 つ分に等しいですから
の長さは波 3 つ分に等しいですから 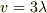 ,
さらに,この 3 とは振動数のことですから
,
さらに,この 3 とは振動数のことですから 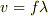 となります.
もっとも,一般的にはこんなにぴったり1秒後に元の位置に戻りませんが,
ぴったりからズレていてもズレた分だけ考えれば同じ結論になります.
となります.
もっとも,一般的にはこんなにぴったり1秒後に元の位置に戻りませんが,
ぴったりからズレていてもズレた分だけ考えれば同じ結論になります.
いちばん基本的な波(正弦波)
どんな揺れ方をしていても,繰り返し同じ形が現れていれば,それを「波」と呼びます. だけど単純な形をしている波だけに話を限った方が,わかりやすいかもしれません. どんな形を単純な形と言っているかというと,次の図のような形です.
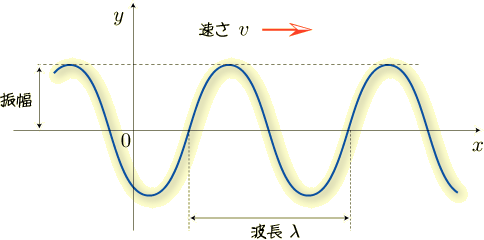
これは原点の動きだけに注目すると,単振動と呼ばれる振動の仕方をしています.
この波の形は 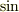 とか
とか 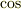 といった三角関数のグラフと同じ形をしているので,このような波を「正弦波」と呼びます.(…余弦波とは呼ばないようです)
といった三角関数のグラフと同じ形をしているので,このような波を「正弦波」と呼びます.(…余弦波とは呼ばないようです)
実は“フーリエ級数で展開する”という操作を行うと,どんな形の波でも,複数の正弦波が重なり合ってできていると考えることができます [‡] . それだけに,正弦波についていろいろと知っておくことは,とても大事なのです.
| [‡] | 三たび正確なことを言い出すと,そのように簡単な重ね合わせができない波も存在します.そういうものを「非線形波」と呼びます. |