波の式2
波の式1 では,波源が原点にあって 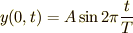 (
( 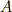 は振幅,
は振幅, 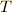 は周期)という振動をしている場合について,
は周期)という振動をしている場合について,  の
領域でどのような振動になっているかを学びました.波の式2では,この場合の
の
領域でどのような振動になっているかを学びました.波の式2では,この場合の 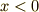 の領域での振動や,
波源の振動が
の領域での振動や,
波源の振動が 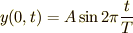 でない場合の振動,そして,波源が原点以外の点にある場合の振動についてみていきます.
以下では,波長を
でない場合の振動,そして,波源が原点以外の点にある場合の振動についてみていきます.
以下では,波長を 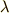 ,波の伝わる速さを
,波の伝わる速さを  とします.
とします.
x<0の領域ではどのような振動になっているか
波源が原点にあって 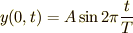 という振動をしている場合,
という振動をしている場合, 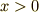 の領域では,
の領域では,
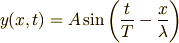
という振動をしていましたね.点  においては,「波源の振動が
においては,「波源の振動が 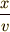 秒遅れて伝わる」
ということから式を導いたのでした.では,
秒遅れて伝わる」
ということから式を導いたのでした.では, 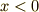 の領域にはどのような振動が伝わっているのでしょうか.
の領域にはどのような振動が伝わっているのでしょうか.
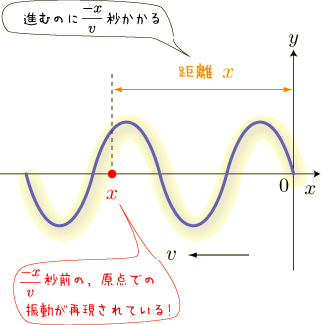
原点にある波源の振動が点  の位置まで伝わるのにかかる時間は,
の位置まで伝わるのにかかる時間は,  秒となります.
なぜ,マイナスがついているか,分かるでしょうか?
今,
秒となります.
なぜ,マイナスがついているか,分かるでしょうか?
今,  は負です.そのため,
は負です.そのため, 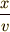 は負になってしまい,
「時間が経過している」ということと矛盾してしまいます.それを避けるために,
マイナスをつけて,値がプラスになるようにしているのです.
は負になってしまい,
「時間が経過している」ということと矛盾してしまいます.それを避けるために,
マイナスをつけて,値がプラスになるようにしているのです.
 秒前の波源の振動が伝わってきているので,
秒前の波源の振動が伝わってきているので, 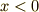 の領域では,
の領域では,
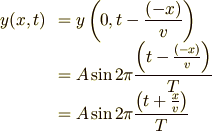
となります.少し書き換えてみますと,
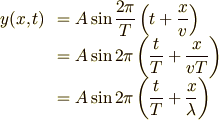
となります.
波源の振動がこれまでと違う場合はどうなるか
これまでは,波源の振動を
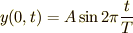
に限ってきました.これは,時刻 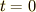 に媒質が点
に媒質が点 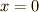 を
を 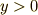 の方向に向かって通過する振動で,
言ってみれば特殊な場合です.しかし,波源は必ずしもそういった振動であるとは限りません.一般に波源の振動は,
の方向に向かって通過する振動で,
言ってみれば特殊な場合です.しかし,波源は必ずしもそういった振動であるとは限りません.一般に波源の振動は,

と表すことができます.この振動では, 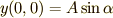 となりますね(
となりますね( 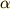 を「初期位相」と呼びます).
さて,このとき点
を「初期位相」と呼びます).
さて,このとき点  ではどのような振動になるでしょうか.波源の振動が,
ではどのような振動になるでしょうか.波源の振動が, 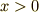 の領域では
の領域では
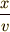 秒だけ遅れて,
秒だけ遅れて, 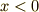 の領域では
の領域では  だけ遅れて伝わることは,
もう分かりますね.したがって,
だけ遅れて伝わることは,
もう分かりますね.したがって, 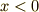 の領域では
の領域では
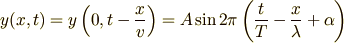
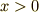 の領域では
の領域では
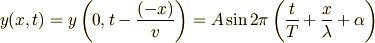
となるわけです.
波源が原点以外の点にある場合はどうなるか
これまでは,波源が原点にある場合を扱ってきました.では,波源が原点以外の点にある場合は,どうなるのでしょうか.
波源が点 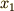 にあって,
にあって,
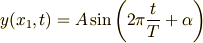
という振動をしている場合を考えてみましょう.
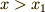 の領域の点
の領域の点  には,波源の振動が
には,波源の振動が 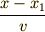 秒遅れて伝わってきます.
秒遅れて伝わってきます.
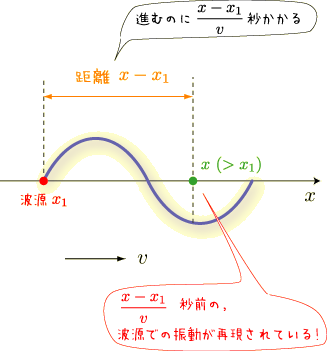
したがって,
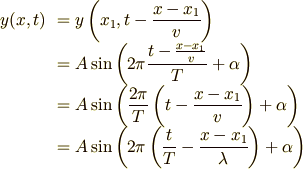
と求まります.
まとめ
波の式を求めるのに考えなければならないことは,
- 波源はどこにあるのか
- 波源はどのような振動をしているか
- 振動の様子を知りたい点には,波源の振動が何秒遅れて伝わってきているか
の3つです.・・・と聞いて,「ふむふむ」と思えた人はもう大丈夫です.
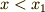 の領域ではどのような振動になるか.
の領域ではどのような振動になるか.