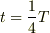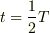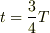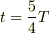波の式1
波動を学んでいると,「波の式」というものが登場します.振動の様子を,式で表してみようというものです.
任意の点  の時刻
の時刻 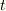 における変位
における変位 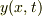 を求めることが目標です.
以下では,変位
を求めることが目標です.
以下では,変位 ![y[{\rm m}]](./577c6ca04447ad69b89df593946f5280.png) や位置
や位置 ![x[{\rm m}]](./78befaa63a51af11ec12b1c49976022c.png) ,時刻
,時刻 ![t[{\rm s}]](./3561d94b4ac71d35620d338eab3c9e6f.png) ,周期
,周期 ![T[{\rm s}]](./bd50a5d3b7c2111103b672ce1d6eeced.png) ,波長
,波長 ![\lambda[{\rm m}]](./e832e4063471a4aa1abd1fd8c58b83ed.png) ,振幅
,振幅 ![A[{\rm m}]](./5484a928fbbc8e6e816149b860d55be8.png) など,波動を学ぶ上で基本的な要素が
出てきます.これらについて勉強が済んでいない人は,まず 波の大事な性質 から読んでみてください.
など,波動を学ぶ上で基本的な要素が
出てきます.これらについて勉強が済んでいない人は,まず 波の大事な性質 から読んでみてください.
原点は単振動している
分かりやすいように,波源は原点にあるとします.そして,その波源は 単振動 しています.
原点での変位 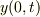 はどのように表せるでしょうか.
はどのように表せるでしょうか.
ここでは周期を 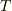 としていますので,
としていますので, ![T[s]](./c4ecd534250af2d17da81b80b699cd55.png) 経過した時に元の変位に戻っていなければなりません.
時刻
経過した時に元の変位に戻っていなければなりません.
時刻 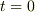 での変位を
での変位を 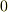 とし,そこから単振動をスタートしたとすると,
とし,そこから単振動をスタートしたとすると,
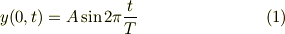
となります. 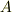 は振幅です.時刻
は振幅です.時刻 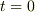 からスタートして,
からスタートして, ![T[s]](./c4ecd534250af2d17da81b80b699cd55.png) 秒後の
秒後の 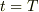 のときに初めて,位相が
のときに初めて,位相が 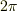 に戻りますね.
つまり,変位が元に戻ってくるということです.ここで,位相が無次元になっていることも確認してください.
(式(1)のより詳細な説明については, 単振動 を参照してください.)
に戻りますね.
つまり,変位が元に戻ってくるということです.ここで,位相が無次元になっていることも確認してください.
(式(1)のより詳細な説明については, 単振動 を参照してください.)
原点の振動が伝わっていく
原点の振動が式(1)のように表されるとき,波はどのように伝わっていくのでしょうか. グラフに描いてみましょう.ひもの先を原点で振動させるようなイメージです. 波源から出た波は,等速で伝わっていきます.

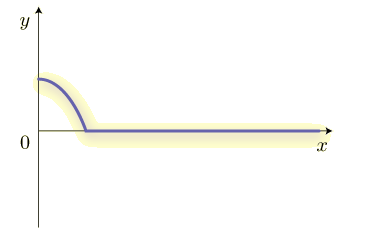
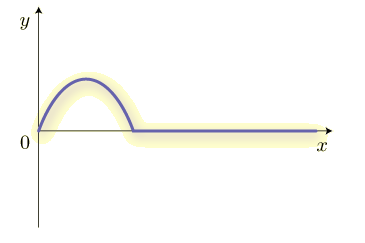
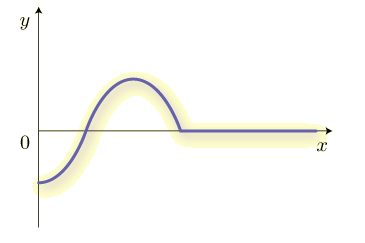
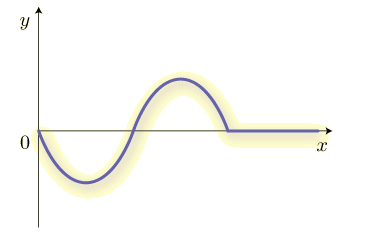
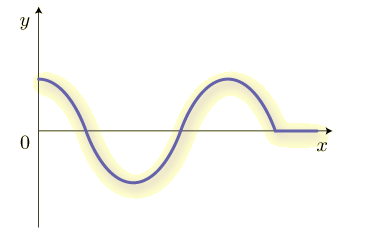
このように伝わっていきますね.原点での振動がだんだんと伝わっていくことが分かります.
上に示したグラフは,  グラフです.つまり,グラフ1枚1枚は時刻
グラフです.つまり,グラフ1枚1枚は時刻 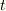 を固定したものだということです.
そして,時刻を追って動かすと,以下のようになります.
を固定したものだということです.
そして,時刻を追って動かすと,以下のようになります.
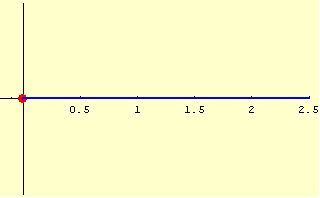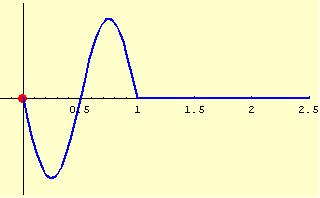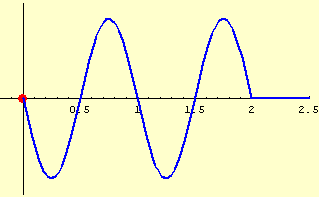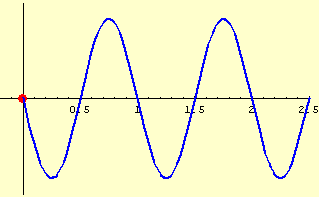
原点以外の点ではどのような振動になるか
では,原点以外の点ではどのような振動になるかをみていきましょう. 波は以下のように伝わっていくのでした.
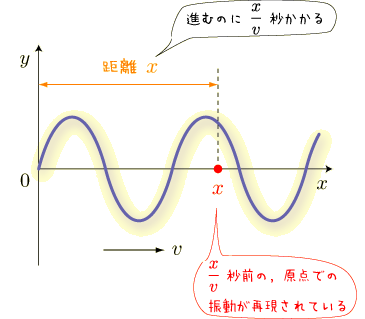
点  にスポットを当てて考えてみます.今,点
にスポットを当てて考えてみます.今,点  にいる波も,
元はといえば原点にいました.何秒か前の原点の振動が再現されているということもできますね.
では,何秒前の原点の振動が再現されているのでしょうか.
波の伝わる速さを
にいる波も,
元はといえば原点にいました.何秒か前の原点の振動が再現されているということもできますね.
では,何秒前の原点の振動が再現されているのでしょうか.
波の伝わる速さを  としますと,原点から点
としますと,原点から点  に到達するまでに
に到達するまでに 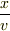 という時間がかかっています(
という時間がかかっています( 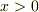 としています).
つまり,
としています).
つまり, 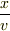 秒前の原点での振動が,今,点
秒前の原点での振動が,今,点  で再現されているのです.
原点は(1)で表される振動をしているわけですから,点
で再現されているのです.
原点は(1)で表される振動をしているわけですから,点  における変位を
における変位を 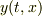 とすると,
とすると,
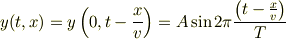
となることが分かります.少し書き換えてみますと,
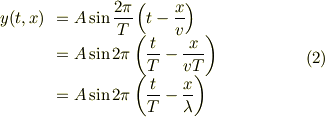
となります( 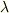 は波長).今まで一生懸命この式を覚えていた!!っていう人,いませんか?
えぇ〜っと・・・
は波長).今まで一生懸命この式を覚えていた!!っていう人,いませんか?
えぇ〜っと・・・ 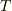 はどこだっけ・・・
はどこだっけ・・・ 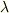 はどこだっけ・・・分子?分母?なんて思い出そうとしていた人,いませんか?
導出はそれほど難しくありませんから,式を覚えるより考え方を身に付けてしまった方が良いですよ.
また,はじめのセクションでも触れましたが,位相は無次元です.(2)式の括弧の中を見てみると,
はどこだっけ・・・分子?分母?なんて思い出そうとしていた人,いませんか?
導出はそれほど難しくありませんから,式を覚えるより考え方を身に付けてしまった方が良いですよ.
また,はじめのセクションでも触れましたが,位相は無次元です.(2)式の括弧の中を見てみると, ![t[{\rm s}]](./3561d94b4ac71d35620d338eab3c9e6f.png) が
が ![T[{\rm s}]](./bd50a5d3b7c2111103b672ce1d6eeced.png) で
割ってありますし,
で
割ってありますし, ![x[{\rm m}]](./78befaa63a51af11ec12b1c49976022c.png) が
が ![\lambda[{\rm m}]](./e832e4063471a4aa1abd1fd8c58b83ed.png) で割ってありますから,ちゃんと無次元になっています.
そういったところを気をつけていると,つまらない間違えをふせげるかもしれません.
で割ってありますから,ちゃんと無次元になっています.
そういったところを気をつけていると,つまらない間違えをふせげるかもしれません.