ドップラー効果3
音源が  軸上,観測者が
軸上,観測者が 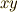 平面上をを等速度運動をしているときのドップラー効果
について考えましょう.波面の時間変化を図に明示するように工夫しているのが特徴です.
同一直線上を等速度運動する場合については tomo さんの分かりやすい解説 [1],[2] が
ありますので,まずそちらをご覧ください.
平面上をを等速度運動をしているときのドップラー効果
について考えましょう.波面の時間変化を図に明示するように工夫しているのが特徴です.
同一直線上を等速度運動する場合については tomo さんの分かりやすい解説 [1],[2] が
ありますので,まずそちらをご覧ください.
一般の場合も相対速度で考えますか?
以下では,音速を 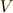 ,時刻
,時刻 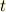 における音源(source)の位置を
における音源(source)の位置を
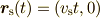 ,観測者(observer)の位置を
,観測者(observer)の位置を
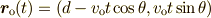 とします.
時刻
とします.
時刻 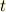 での音源の振動を
での音源の振動を
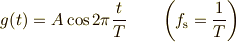
とすると,時刻 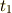 に音源から出た音の波面(位相が等しい点の集合)は,中心が
に音源から出た音の波面(位相が等しい点の集合)は,中心が
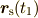 ,半径が
,半径が 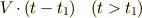 の
球面となって空間に拡がります.この波面が観測者に届く時刻を
の
球面となって空間に拡がります.この波面が観測者に届く時刻を 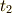 とすると,
とすると,
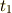 ,
, 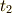 の間には
の間には
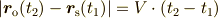
という関係が成立しているはずです.また  に音源から出た音の波面が
観測者に届く時刻を
に音源から出た音の波面が
観測者に届く時刻を 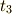 とおくと,
とおくと,  が観測者が聴く音の周期
(振動数の逆数)になります.
が観測者が聴く音の周期
(振動数の逆数)になります.
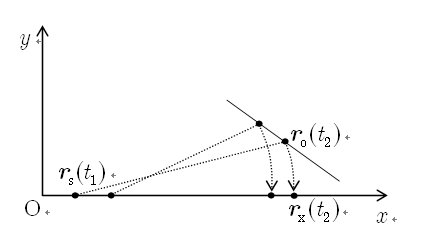
 軸上の同位相の点
軸上の同位相の点
一般に,時刻 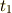 ,
, 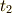 に観測者と同じ波面が届く
に観測者と同じ波面が届く  軸上の点は
上図のような円弧と
軸上の点は
上図のような円弧と  軸の交点で求まりますが,
軸の交点で求まりますが,

のときは,これらの円弧を  軸に垂直な線分とみなすと [*] ,よく知られた
観測者が聴く音の振動数
軸に垂直な線分とみなすと [*] ,よく知られた
観測者が聴く音の振動数 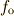 の近似式
の近似式
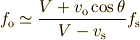
が得られます.この式を導くとき,通常 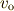 によって音の相対速度が変わる
として説明しています.この説明は波面を平面波で近似できるときは分かりやすいのですが,
上図から予想できるように,平面波で近似しないときまで相対速度にこだわると収拾が
つかなくなります.
によって音の相対速度が変わる
として説明しています.この説明は波面を平面波で近似できるときは分かりやすいのですが,
上図から予想できるように,平面波で近似しないときまで相対速度にこだわると収拾が
つかなくなります.
| [*] | 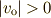 , , 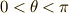 として,右辺を底辺の長さ,
左辺を高さとする三角形を考えてください. として,右辺を底辺の長さ,
左辺を高さとする三角形を考えてください. |
同一直線上を移動するときの時空間モデル
ここでは一般化のための準備として,「相対速度」を考えない(音速はいかなる場合も 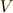 であるとした)モデルで
であるとした)モデルで 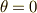 のときのドップラー効果の公式を導く方法を示します.
のときのドップラー効果の公式を導く方法を示します.
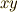 平面上に波面を描いた図はドップラー効果の本質を理解する上では重要ですが,
通常は一つの時刻における波面しか表していないので(二つの時刻の波面を重ね合わせた
だけでも左側の図のように見にくくなります),波面が時間的に拡がっていくようすは
頭の中で想像しなければなりません.しかし,観測者が聴く音の振動数(あるいはその逆数の
周期)を求める計算では,
平面上に波面を描いた図はドップラー効果の本質を理解する上では重要ですが,
通常は一つの時刻における波面しか表していないので(二つの時刻の波面を重ね合わせた
だけでも左側の図のように見にくくなります),波面が時間的に拡がっていくようすは
頭の中で想像しなければなりません.しかし,観測者が聴く音の振動数(あるいはその逆数の
周期)を求める計算では,  軸上の波の位相だけを考えれば十分です.このため,
軸上の波の位相だけを考えれば十分です.このため,
 軸と垂直に
軸と垂直に 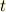 軸をとって
軸をとって  軸上の波の位相の時間的変化を図示した右側の図のような
モデルを考えます.
軸上の波の位相の時間的変化を図示した右側の図のような
モデルを考えます.
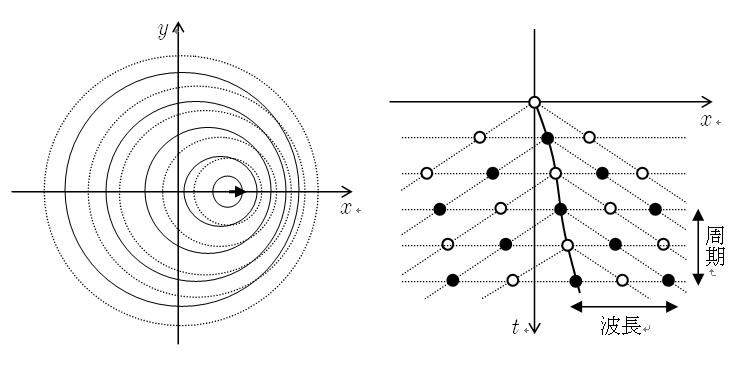
 軸上の波面の時間変化
軸上の波面の時間変化
分かりやすいように,この図では 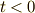 で出された音の波面は描いていません.また,等速度
運動でなくても同じように考えてよいことを強調するために,音源の加速度を少し変えています.
図の白丸は波面の位相が
で出された音の波面は描いていません.また,等速度
運動でなくても同じように考えてよいことを強調するために,音源の加速度を少し変えています.
図の白丸は波面の位相が 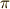 の偶数倍,黒丸は
の偶数倍,黒丸は 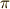 の奇数倍の点であり,
の奇数倍の点であり,  軸方向に
隣接する白丸(あるいは黒丸)間の距離が波長を,
軸方向に
隣接する白丸(あるいは黒丸)間の距離が波長を, 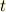 軸方向に隣接する白丸(あるいは黒丸)
間の距離が音源の出す音の周期を表しています(半周期の整数倍の時刻のみ位相を表示していますが,
点線上の位相はすべて白丸,またはすべて黒丸です).音源が
軸方向に隣接する白丸(あるいは黒丸)
間の距離が音源の出す音の周期を表しています(半周期の整数倍の時刻のみ位相を表示していますが,
点線上の位相はすべて白丸,またはすべて黒丸です).音源が  軸方向に動いているときは
音源より右側の波長が長くなり,左側の波長が短くなっているのがわかりますね.以下では
この図を時空間モデルということにしましょう.
軸方向に動いているときは
音源より右側の波長が長くなり,左側の波長が短くなっているのがわかりますね.以下では
この図を時空間モデルということにしましょう.
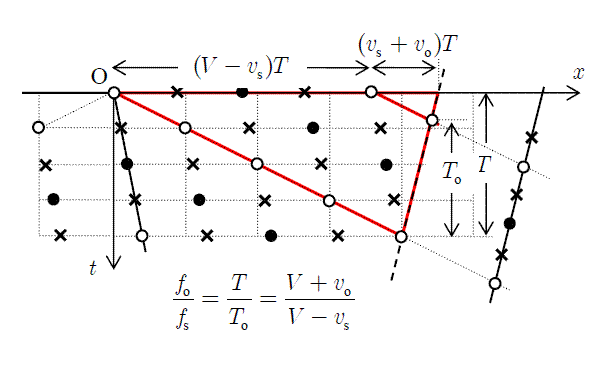
時空間モデルによる公式の導出
上図は音源,観測者が最初に述べた等速度運動しているときの時空間モデルです.図の左端の斜線は
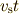 のグラフ,右端の斜線は
のグラフ,右端の斜線は 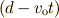 のグラフです.この図では観測者が
音源のすぐそばにいるとした非現実的な場合を描いていますが,遠くにいるときも同様です.観測者が
聴く音の周期を求めるには,観測者の軌跡を図の破線の位置まで平行移動して考えます.
のグラフです.この図では観測者が
音源のすぐそばにいるとした非現実的な場合を描いていますが,遠くにいるときも同様です.観測者が
聴く音の周期を求めるには,観測者の軌跡を図の破線の位置まで平行移動して考えます.
 軸上の線分とこの破線上の線分を2辺とする二つの相似な三角形について
軸上の線分とこの破線上の線分を2辺とする二つの相似な三角形について
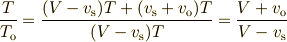
が成立することはただちに分かります.これがよく知られたドップラー効果の公式です.この図で
あれば,観測者が等速度で運動していないときでも 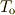 は容易に求められますね.相対速度
で考えるとどうでしょう?
は容易に求められますね.相対速度
で考えるとどうでしょう?
観測者が聴く音の周期の求め方
最初に説明したように,  軸上に
軸上に 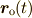 と同位相の点
と同位相の点 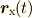 が分かれば,(短い区間では等速度で運動していると近似して)観測者が聴く音の周期を求める
ことができます.
が分かれば,(短い区間では等速度で運動していると近似して)観測者が聴く音の周期を求める
ことができます.
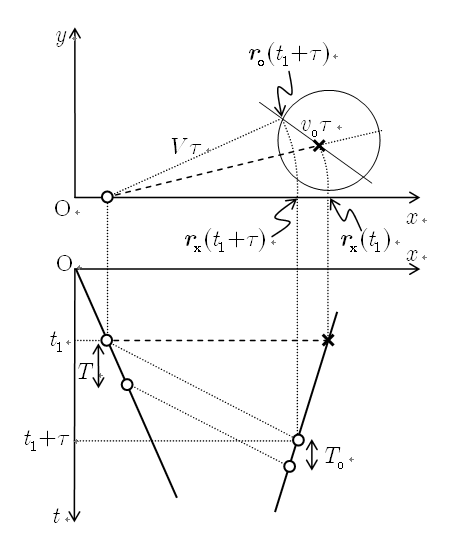
 軸上の同位相の点を用いた周期の計算
軸上の同位相の点を用いた周期の計算
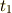 が与えられたとき,
が与えられたとき,
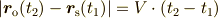
となる 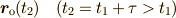 は
は
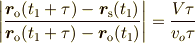
より, 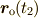 は2点
は2点 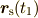 ,
, 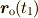 までの
距離の比が
までの
距離の比が 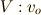 となるアポロニウスの円と観測者の軌跡の交点上にあることが分かります.
したがって,
となるアポロニウスの円と観測者の軌跡の交点上にあることが分かります.
したがって, 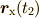 は,中心が
は,中心が 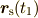 , 半径が
, 半径が
 の円と
の円と  軸の交点です.
軸の交点です.
通常は 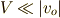 なので,
なので, 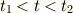 の付近では等速度であるとして,観測者の
軌跡を直線で近似すると前述の方法で時刻
の付近では等速度であるとして,観測者の
軌跡を直線で近似すると前述の方法で時刻 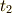 に観測者が聴く音の周期を求めることができます.
この近似の誤差が大きいときは,
に観測者が聴く音の周期を求めることができます.
この近似の誤差が大きいときは, 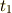 より少し前の時刻
より少し前の時刻 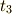 について同様の処理を行い,
について同様の処理を行い,
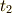 に対応する時刻
に対応する時刻 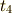 を求めて
を求めて 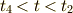 の付近では等速度であると近似すること
により,精度を上げることができます.
の付近では等速度であると近似すること
により,精度を上げることができます.
あとがき
本資料で述べた一般化に実用的価値はあまりありませんが,モデリングについて 所属学会の研究会で発表した内容を補足して紹介しました.与えられた課題を 解く際に,何が本質的に重要かを考える一例として参考になれば幸いです.