四次元空間中のベクトルの回転
この記事では,Joh氏の ベクトルの回転 を拡張して四次元空間中での回転を考えます.
特殊な場合
四次元空間中の回転では,回転軸が二つに
なり, 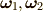 となります.
簡単のため,それらは正規直交化されているものとします.
一番明らかな回転は,回転軸が
となります.
簡単のため,それらは正規直交化されているものとします.
一番明らかな回転は,回転軸が
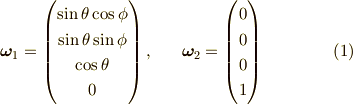
の時です.これは,四番目の次元の方向  にまず直交し,
二次元球面の極座標表示の示す方向に対しても直交する回転です.
にまず直交し,
二次元球面の極座標表示の示す方向に対しても直交する回転です.
つまり,先に言いましたが,四番目の次元方向  に直交していても,それに直交する単位ベクトル
に直交していても,それに直交する単位ベクトル 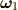 をとれることが分かるでしょう.
をとれることが分かるでしょう.
一般化
Joh氏の ベクトルの回転 を一般化します. 拡張すべき式は,
![\bm{r}^\prime = (\bm{n} \cdot \bm{r})\bm{n} + [\bm{r}-(\bm{n} \cdot \bm{r})\bm{n}]\cos \eta - (\bm{r} \times \bm{n})\sin \eta \tag{2}](./b50997fb968dfb7ff77e984d1bc9ebe4.png)
です.四次元の任意のベクトル  を
回転軸
を
回転軸

の周りに角度 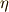 だけ回転した
ベクトルを
だけ回転した
ベクトルを  とするのです.
注意深く考えると,回転軸の方向にはいくら回転しても,値が変化することはありません.
よって,その方向の自由度を奪って回転面内のベクトルにしてしまいましょう.それには,
とするのです.
注意深く考えると,回転軸の方向にはいくら回転しても,値が変化することはありません.
よって,その方向の自由度を奪って回転面内のベクトルにしてしまいましょう.それには,
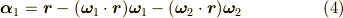
を考えれば,回転面内のベクトルで回転の始点となるベクトル
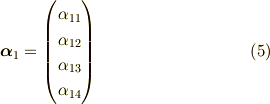
ができます.後は,回転面内で 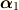 に直交するベクトルを
に直交するベクトルを  と置いて,
と置いて, 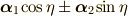 としてやれば良さそうですね. [*] この
としてやれば良さそうですね. [*] この  は,回転面内と言うところがポイントです.つまり,
は,回転面内と言うところがポイントです.つまり,  は,
は, 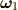 ,
,  ,
, 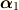 の全てに直交しているのです.
これは次の様に求まります.
の全てに直交しているのです.
これは次の様に求まります. 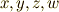 軸方向の単位ベクトルを
軸方向の単位ベクトルを 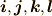 とすると,行列式の記法で,
とすると,行列式の記法で,
| [*] | 三次元では三つのベクトルに対して右手系と左手系が定義されていますが,四次元では標準の様なものが無いので, 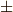 を決定できません. を決定できません. |

となります.そんなに怖いものではありません.例えば,  と,
と, 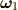 の内積をとると,式
の内積をとると,式 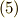 の第一行目が
の第一行目が 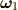 に置き換わります.つまり,同じ行が第二行目にあるので式の値はゼロとなり,直交していることが分かります.これで,無事
に置き換わります.つまり,同じ行が第二行目にあるので式の値はゼロとなり,直交していることが分かります.これで,無事 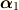 と
と  が求まったので,回転が記述できます.
が求まったので,回転が記述できます.
それは,
![\bm{r}^\prime &= (\bm{\omega}_1 \cdot \bm{r}) \bm{\omega}_1 + (\bm{\omega}_2 \cdot \bm{r}) \bm{\omega}_2 + [ \bm{r}- (\bm{\omega}_1 \cdot \bm{r}) \bm{\omega}_1 - (\bm{\omega}_2 \cdot \bm{r}) \bm{\omega}_2 ] \cos \eta \pm\begin{vmatrix}\bm{i} & \bm{j} & \bm{k} & \bm{l} \\\omega_{11} & \omega_{12} & \omega_{13} & \omega_{14} \\\omega_{21} & \omega_{22} & \omega_{23} & \omega_{24} \\\alpha_{11} & \alpha_{12} & \alpha_{13} & \alpha_{14} \end{vmatrix} \sin \eta \\ &= (\bm{\omega}_1 \cdot \bm{r}) \bm{\omega}_1 + (\bm{\omega}_2 \cdot \bm{r}) \bm{\omega}_2 + \bm{\alpha}_1 \cos \eta \pm \bm{\alpha}_2 \sin \eta\tag{7}](./df5b84a06e003c52d6e082075810dd72.png)
となります.
四次元以上への拡張は容易ですね.五次元なら,回転の軸を正規直交した 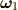 ,
,  ,
, 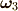 にすればいいのです.行列式は,これプラス
にすればいいのです.行列式は,これプラス 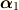 を用いる5×5の行列式になります.
を用いる5×5の行列式になります.
今日はここまで,お疲れさまでした.