ベクトル空間と線形写像
ベクトルと聞くと,矢印をイメージする人が多いかも知れません.この記事では,その図形的なイメージを離れて,ベクトルの持つ性質を高度に抽象化した ベクトル空間 という概念を勉強します.
どうも『空間』という言葉に馴染まない人は,慣れるまで,空間を『集合』と読み替えながら読み進んでも大丈夫です.この後に出てくる空間という言葉は,たいてい集合の意味です.この記事の議論では,ベクトルの概念を,矢印とは似ても似つかないものをも含む一般的な概念にまで拡張します.まずここで,図形的な矢印のイメージは潔く捨てて下さい!

『矢印のイメージは捨てるのじゃ!』
...とは言っても,覚えたり理解するための助けとして,幾何学的なイメージを使うことはあります.
ベクトルの演算
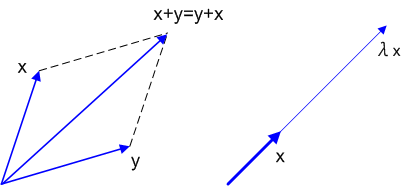
幾何ベクトルの演算には,次のような著しい特徴がありました.図では 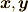 をベクトル,
をベクトル, 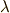 をスカラーとしています.
をスカラーとしています.
- 和に関して可換(順序交換可能)であり,ベクトルの和はベクトルになる.
- ベクトルのスカラー倍はベクトルになる.
さらに,スカラー倍とベクトルの和に関して,分配則がなりたちます.
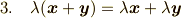
ベクトルの計算を知っている人にとっては,なかば当たり前の性質ですね.しかし,この三つの性質はあとで重要になります.覚えておいて下さい.
ベクトル空間
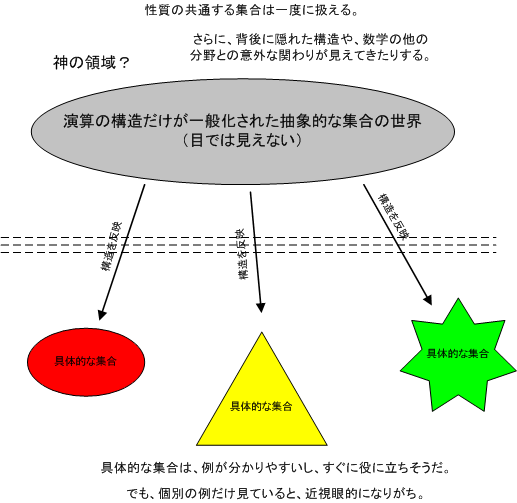
ベクトル空間とは集合です.ただの集合ではなく,集合の元の間に『加法』と『スカラー積』と言われる演算が定義されています.これは,簡単に言えば前セクションでみた 幾何ベクトルの演算規則だけに着目し,概念を一般化したもの だと言えます.
一般化とはどういうことかと言えば,幾何ベクトルに限らず,『加法とスカラー積の演算規則を満たす集合なら何でもよい』ということです.具体的に集合の元が何か,ということは問わないのです.こうすることで,同じ算法を満たすものは何であれ,全て同一の議論で一緒くたに扱ってしまえます.抽象数学の強味です.
| [*] | ベクトルのイメージが矢印でないとすれば,もはやこのようなベクトルの加法は『ベクトルとベクトルを足すと平行四辺形の対角線になる』というイメージの加法とも程遠いものになるでしょう.ベクトルの足し算と聞いて,平行四辺形を思い浮かべるレベルを早く脱却しないといけません. |
細かな定義
加法とスカラー積を満たすと言っても,数学的にこの意味をもう少しきちんと決めておく必要があります.加法とスカラー積を行うために必要とされる演算規則を細かく書き出すと,以下の 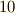 個の条件になります.これら個別の条件を丸暗記することには,あまり意味がありません.『 加法とスカラー積 』という二つの演算を念頭に置いていれば,だいたい自然にこれらの条件を挙げられるものですので,そのような視点で一つ一つ確認してみて下さい.
個の条件になります.これら個別の条件を丸暗記することには,あまり意味がありません.『 加法とスカラー積 』という二つの演算を念頭に置いていれば,だいたい自然にこれらの条件を挙げられるものですので,そのような視点で一つ一つ確認してみて下さい.
ベクトル空間を 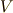 と書き,
と書き, 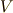 の元を
の元を 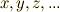 のようにアルファベットで表わします.太字で書くことはやめます.また,
のようにアルファベットで表わします.太字で書くことはやめます.また, 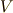 の元とは別に何か,スカラー積に使うスカラーが必要ですが,スカラーはギリシャ文字で
の元とは別に何か,スカラー積に使うスカラーが必要ですが,スカラーはギリシャ文字で 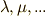 のように書き,数の集合
のように書き,数の集合 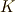 の元だとします.
の元だとします. 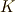 は具体的には,
は具体的には, 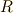 (実数)や
(実数)や 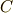 (複素数)などです.
(複素数)などです.
【ベクトル空間の公理】
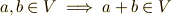 (加法が閉じている)
(加法が閉じている)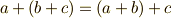 (加法の結合則)
(加法の結合則)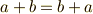 (加法の交換則)
(加法の交換則)- 加法の零元
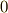 が存在する.
が存在する. 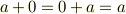
- 加法の逆元が存在する.
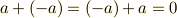
- 任意のスカラー
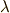 に対して
に対して 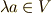 (スカラー積が閉じている)
(スカラー積が閉じている) 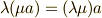 (スカラー積の結合則)
(スカラー積の結合則)- スカラー積の零元
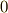 が存在する.
が存在する. 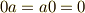
- スカラー積の単位元
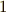 が存在する.
が存在する. 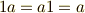
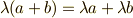 (スカラー積と加法の分配法則)
(スカラー積と加法の分配法則)
正確を期して,スカラー積の演算に使うスカラーがどのような数かによって『○○ベクトル空間』と言う場合もあります.例えばスカラーが実数なら実ベクトル空間,複素数なら複素ベクトル空間といった具合です.もっと一般には,スカラーの種類を言うのに『〜上の』という表現を使って,例えば実ベクトル空間を『 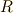 上のベクトル空間』と言ったりもします.いま私たちは,あまり詳しい用語にこだわる必要はないでしょう.
上のベクトル空間』と言ったりもします.いま私たちは,あまり詳しい用語にこだわる必要はないでしょう.
| [†] | 単位元,零元,逆元などが個別の条件として色々出てきましたが,現代の代数学では,こうしたものが有るか無いかがとても大事なのです.何でそんなことに細かくこだわるんだ?と思った人は, 群の公理 などを読んでみて下さい.また,上記の条件は公理ではなくて定義なんではないかと思う考える人もいると思いますが,代数構造は公理的に与えられる,と考えるのが現代数学風です. |
繰り返しになりますが,ベクトル空間の演算規則とは, 最初に見た幾何ベクトルの3つの演算規則(加法,スカラー積,分配則)を抽象化したものに他なりません .前節の二つの絵に,全ては集約されています.矢印のイメージに囚われてはいけませんが,記憶の助けとして前セクションの幾何ベクトルの絵を使えば,かなり楽に覚えられるのではないかと思います.
これも繰り返しになりますが,ベクトル空間とは抽象的な概念だという点が重要です.条件 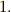 〜
〜 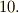 を満たす物の集合ならば,幾何ベクトルとは似ても似つかない物の集合がベクトル空間になっても良いわけです.似ても似つかないって言われたって・・・,そんなの想像できませんが,逆に想像できないような物まで一気にカバー出来てしまうことが嬉しいのだと諒解してください.
を満たす物の集合ならば,幾何ベクトルとは似ても似つかない物の集合がベクトル空間になっても良いわけです.似ても似つかないって言われたって・・・,そんなの想像できませんが,逆に想像できないような物まで一気にカバー出来てしまうことが嬉しいのだと諒解してください.
しかし,そもそもなぜベクトルの 算法だけ を一般化した抽象的な集合なんて考えるんでしょうか?そのような抽象数学は,すぐ目の前にある計算の役には立たなそうです.しかし,ベクトルの算法だけを一般化した集合(普通の幾何ベクトルもこの集合の一種になるわけです)の性質を調べることで,意外にもベクトルの計算の舞台となっている世界のカラクリとでもいうものが見えてくるかも知れません.そういった大きな視点で知識を整理すると頭がすっきりします.抽象数学は無駄なものを取り去った非常にシンプルな形で,そういった数学的な構造をまざまざと見せてくれます.
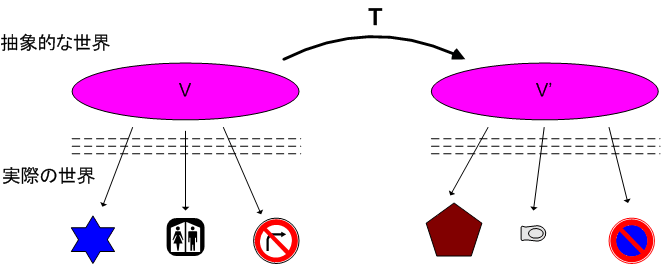
線形写像
あるベクトル空間 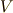 を,別のベクトル空間
を,別のベクトル空間 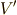 へ対応させる写像
へ対応させる写像 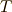 を考えます.
を考えます.
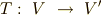
写像のことを関数と呼んでも良いでしょう.何か 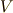 の元(仮に
の元(仮に  としましょう)を一個取ってきて関数
としましょう)を一個取ってきて関数 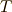 に放り込むと,
に放り込むと, 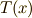 は
は 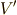 の元になってしまうということです.
の元になってしまうということです. 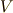 と
と 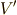 が同じ次元でなくても構いません.
が同じ次元でなくても構いません.
この写像がさらに次の性質を満たすとき,これを 線形写像 と言います. 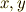 は
は 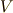 の元,
の元, 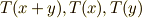 は
は 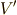 の元だということに注意してください.
の元だということに注意してください.  は適当なスカラーとします.
は適当なスカラーとします.
【線形写像の満たす性質】
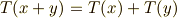
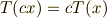
線形写像により,ベクトル空間 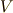 の元同士の加法とスカラー積,つまり
の元同士の加法とスカラー積,つまり 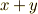 と
と 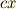 という演算を,
という演算を, 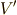 上の演算
上の演算 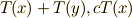 に対応させることが出来ます.つまり,ベクトル空間の元の持つ,線形性という性質が保存されることになります.
に対応させることが出来ます.つまり,ベクトル空間の元の持つ,線形性という性質が保存されることになります.
翻訳という作業も写像ですね.(あまり本文と関係ありません.)