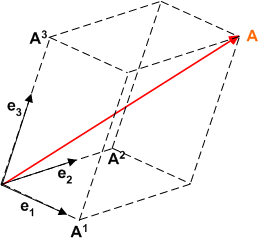
ベクトルの成分を表わす
まず,任意のベクトル 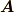 を『長さが
を『長さが 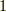 で,互いに直交するベクトル
で,互いに直交するベクトル 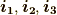 』を基底として成分表示することを考えましょう.
』を基底として成分表示することを考えましょう.
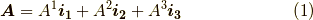
基底ベクトル 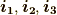 の添字を右下に書いていますので,座標成分の添字を
の添字を右下に書いていますので,座標成分の添字を 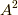 のように右上に書きました.文脈から間違えないとは思いますが,これを『
のように右上に書きました.文脈から間違えないとは思いますが,これを『 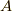 の二乗』と読まないように注意して下さい.
の二乗』と読まないように注意して下さい.
| [*] | 双対基底 の記事で勉強したように,基底ベクトルには添字の上下で 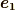 , , 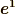 という二つがありました.どちらを基底ベクトルに選んでも良いのですが,基底ベクトルと座標成分の添字は『上と下』もしくは『下と上』と別々になるように決めました.本当は,いま考えているように基底ベクトルが直交する場合,添字の上下の区別は関係なくなります.( 双対基底の図形的関係 参照.)このように約束すると便利なことは, 計量テンソル で勉強します. という二つがありました.どちらを基底ベクトルに選んでも良いのですが,基底ベクトルと座標成分の添字は『上と下』もしくは『下と上』と別々になるように決めました.本当は,いま考えているように基底ベクトルが直交する場合,添字の上下の区別は関係なくなります.( 双対基底の図形的関係 参照.)このように約束すると便利なことは, 計量テンソル で勉強します. |
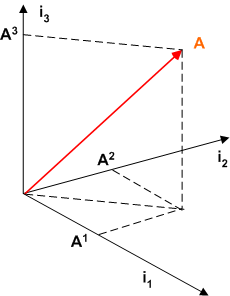
図のように,各成分  は
は 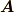 を各軸に射影した長さです.いま基底ベクトルは直交していますから,基底ベクトル
を各軸に射影した長さです.いま基底ベクトルは直交していますから,基底ベクトル 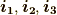 と各辺が平行である直方体の対角線に
と各辺が平行である直方体の対角線に 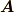 を取るとき,成分
を取るとき,成分 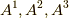 は直方体の各辺の長さに当たります.
は直方体の各辺の長さに当たります. 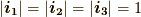 に注意すると,射影した長さは内積を使って次のように表せるでしょう.(ベクトルの射影は もう一度ベクトル を参照ください.)
に注意すると,射影した長さは内積を使って次のように表せるでしょう.(ベクトルの射影は もう一度ベクトル を参照ください.)
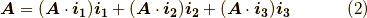
基底ベクトル 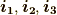 の取り方は,どのような向きでも良いことに注意してください.
の取り方は,どのような向きでも良いことに注意してください.

(どの座標系からベクトルを見ても良い.見え方は変わるけど,同じベクトル.)
ベクトル 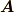 の各成分を,
の各成分を, 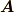 と基底ベクトル
と基底ベクトル 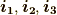 だけで表現することが出来たことを確認して下さい.
だけで表現することが出来たことを確認して下さい.
基底ベクトルの長さが 1 ではない場合
先ほどは 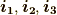 の条件として『長さが
の条件として『長さが  で互いに直交するもの』と定めました.この前半の条件を外し,直交はするが長さは
で互いに直交するもの』と定めました.この前半の条件を外し,直交はするが長さは  とは限らないベクトル
とは限らないベクトル  を基底に取ることを考えます.
を基底に取ることを考えます.
何のことはない,絶対値で割ることで, 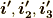 から単位ベクトル
から単位ベクトル 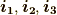 を作ることが出来ます.
を作ることが出来ます.

あとはこの関係を式  に代入するだけです.
に代入するだけです.
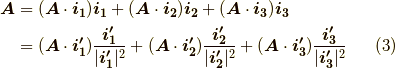
この場合も,各成分を 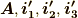 だけで表現することが出来ました.
だけで表現することが出来ました.
基底が直交していない場合
ここまでの議論は,高校数学の範囲でも十分に理解できる内容だったと思います.この節では,最後に基底ベクトルが直交していない場合を考えます.(ただし,基底ベクトルは一次独立だとします.このように直交しない基底ベクトルの取り方を アフィン基底 と呼びます.)
この場合は,基底 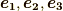 と各軸が平行となる平行六面体の対角線に
と各軸が平行となる平行六面体の対角線に 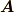 を置いた場合の,平行六面体の辺の長さが
を置いた場合の,平行六面体の辺の長さが 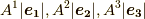 になります.( 双対基底の図形的関係 参照.)
になります.( 双対基底の図形的関係 参照.)
この基底 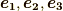 は,一次独立であれば直交していなくても良く,長さも
は,一次独立であれば直交していなくても良く,長さも 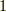 でなくても構いません.いわば,これが一番 一般的なベクトルの成分分解 の形です.
でなくても構いません.いわば,これが一番 一般的なベクトルの成分分解 の形です.
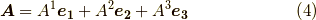
この場合も,さきほどのように成分 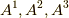 を,ベクトル
を,ベクトル 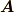 と基底ベクトル
と基底ベクトル 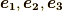 だけを使って表現できるのでしょうか.実は, 双対基底 を使うと鮮やかに
だけを使って表現できるのでしょうか.実は, 双対基底 を使うと鮮やかに 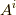 を表現できてしまうのです.
を表現できてしまうのです.
式 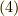 の両辺に,
の両辺に, 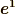 の内積を取ってみましょう.
の内積を取ってみましょう.
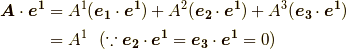
同様にして, 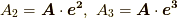 が分かります.そこで式
が分かります.そこで式 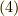 を次のように書き換えられます.
を次のように書き換えられます.
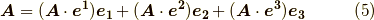
アフィン基底のベクトルの成分も,双対基底を使って簡単に表現できてしまいました.式 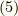 を,この記事の一番最初で考えた式
を,この記事の一番最初で考えた式  と比べてみましょう.
と比べてみましょう.
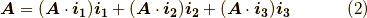
式  と式
と式 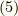 が基本的には同じ構造をしていることが見て分かります.しかし,式
が基本的には同じ構造をしていることが見て分かります.しかし,式  で使った基底
で使った基底 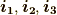 には『長さが
には『長さが 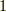 で,互いに直交する基底』という,なかなか厳しい条件がついていました.一方,式
で,互いに直交する基底』という,なかなか厳しい条件がついていました.一方,式 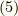 の基底
の基底 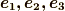 は『一次独立』であること以外,向きも長さも何も決めていません.
は『一次独立』であること以外,向きも長さも何も決めていません.
直交する基底では,双対基底は自分自身になりますので( 双対基底 参照),式 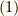 で
で 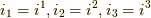 の関係に注意すれば,式
の関係に注意すれば,式  は式
は式 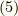 の特別な場合であり,逆に式
の特別な場合であり,逆に式 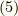 は式
は式  を一般の基底にまで拡張した式になっていまることが分かると思います.
を一般の基底にまで拡張した式になっていまることが分かると思います.
もう一度,ここまでの議論を読み返し,この結果の美しさを味わうとともに,双対基底とはいったい何なのか,自分なりにじっくり考えてみて下さい.
| [†] | この記事までは,なぜ双対基底なんか考えるの?と思っていた人がいたと思います.この記事で見たように,双対基底は,一般に長さが正規化されておらず,直交もしていない基底による表現で威力を発揮します.高校数学では,基底として常に長さが 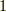 で互いに直交するベクトルばかりを選んでいましたので,双対基底を考える必要がありませんでしたし,そもそも正規直交基底では二つの双対基底は同一になってしまうので区別さえできないのです.私たちは,特定の座標系に縛られることなく,自由自在に視点を変換して良いのですから,双対基底を使った一般的な表現が便利です. で互いに直交するベクトルばかりを選んでいましたので,双対基底を考える必要がありませんでしたし,そもそも正規直交基底では二つの双対基底は同一になってしまうので区別さえできないのです.私たちは,特定の座標系に縛られることなく,自由自在に視点を変換して良いのですから,双対基底を使った一般的な表現が便利です. |