ベクトル・ポテンシャル
ベクトル場 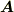 を,次のようにベクトル
を,次のようにベクトル 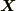 の回転によって表現できるとき,
の回転によって表現できるとき, 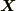 を
を 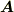 の ベクトル・ポテンシャル と呼びます.
の ベクトル・ポテンシャル と呼びます.

ポテンシャル関数という意味では,ベクトル場には スカラーポテンシャル というものもあることは覚えていると思います.スカラーポテンシャルは一つのスカラー関数で,ベクトル関数よりも扱いやすいですから,ベクトル場をスカラーポテンシャルで表現することにはそれなりに便利な点があります.しかし,ベクトルポテンシャルはベクトルポテンシャル自身がベクトル場ですから,それでベクトル場を表現しても,それほど手間は変わりません.
そんなことが理由なのか分かりませんが,ベクトル解析の教科書を何種類か当てってみても,スカラーポテンシャルに比べてベクトルポテンシャルの扱いが不当に小さいような印象を受けます.物理の問題では,スカラーポテンシャルに負けず劣らず,ベクトルポテンシャルが重要な場合がありますから,やはりきちんと理解しておいた方が良いと思います.
| [*] | 電磁気学では,磁束密度ベクトルを  と表現でき,この と表現でき,この 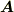 を電磁ポテンシャルと呼ぶことがあります.これは,ベクトルポテンシャルの例です.ただし,これは古風な表現で, divrot=0 より,電磁ポテンシャルなどを使わずに を電磁ポテンシャルと呼ぶことがあります.これは,ベクトルポテンシャルの例です.ただし,これは古風な表現で, divrot=0 より,電磁ポテンシャルなどを使わずに 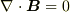 と表記するのが現在の主流です.(これは,電磁気学の基礎方程式の一つとして,マックスウェル方程式の一つになっています.)電磁誘導の式も と表記するのが現在の主流です.(これは,電磁気学の基礎方程式の一つとして,マックスウェル方程式の一つになっています.)電磁誘導の式も 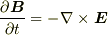 のように書かれますから,これもベクトルポテンシャルだと見ることが可能です.興味のある人は,電磁気学の教科書を当たって見て下さい.ベクトルポテンシャルに関して,数学的に重要なのは ヘルムホルツの定理 です. のように書かれますから,これもベクトルポテンシャルだと見ることが可能です.興味のある人は,電磁気学の教科書を当たって見て下さい.ベクトルポテンシャルに関して,数学的に重要なのは ヘルムホルツの定理 です. |
ベクトルポテンシャル
デカルト座標系でベクトル場 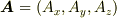 を考えます.
を考えます. 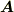 がベクトルポテンシャルのみを使って
がベクトルポテンシャルのみを使って 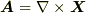 と表現できるとき,次式で与えられるベクトル場
と表現できるとき,次式で与えられるベクトル場 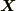 は
は 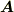 のベクトルポテンシャルになっています.ただし,
のベクトルポテンシャルになっています.ただし, 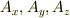 はそれぞれ
はそれぞれ 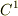 級の関数とします.
級の関数とします.
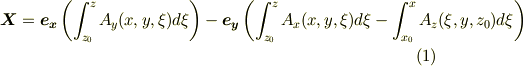
本当に,この 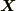 が
が 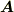 のベクトルポテンシャルになっていることは,直接式
のベクトルポテンシャルになっていることは,直接式 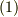 に代入して確かめてみて下さい.なんだか,天下り的になってしまってスミマセン.
に代入して確かめてみて下さい.なんだか,天下り的になってしまってスミマセン.
練習問題
(1)ベクトル場 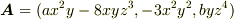 が,ベクトルポテンシャルを用いて
が,ベクトルポテンシャルを用いて 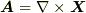 と書けるように,定数
と書けるように,定数 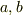 を決定して下さい.(ヒント:
を決定して下さい.(ヒント: 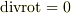 が必要ですね.)
が必要ですね.)
(2)ベクトルポテンシャルには,スカラー関数の勾配 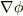 分だけの差は許されること,つまり,
分だけの差は許されること,つまり, 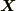 がベクトルポテンシャルならば,
がベクトルポテンシャルならば, 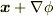 もベクトルポテンシャルになることを確認して下さい.
もベクトルポテンシャルになることを確認して下さい.
(3)ベクトル場 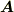 のベクトルポテンシャルを求めて下さい.
のベクトルポテンシャルを求めて下さい.