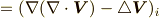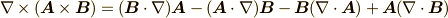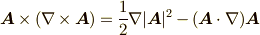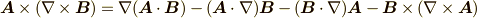テンソル記号を使ってベクトルの公式を導く
微分演算子の演算( 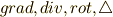 )を,テンソル記号を用いて表わすと次のようになります.添字は
)を,テンソル記号を用いて表わすと次のようになります.添字は 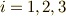 等とし,同じ添字が二回出てきた場合(二乗を含む)は,縮約によってその添字の総和を取るものとします.
等とし,同じ添字が二回出てきた場合(二乗を含む)は,縮約によってその添字の総和を取るものとします.

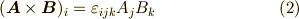


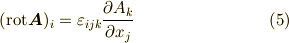

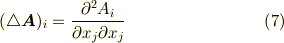
式  は計算の基本になりますから,自分でスラスラ書けないと困ります.各式の左辺の意味がわかっていれば,テンソル記号表記の右辺を導くのは簡単だと思います.また,クロネッカーのデルタやレヴィ・チヴィタ記号の公式も必要になりますので,ここに紹介しておきます.
は計算の基本になりますから,自分でスラスラ書けないと困ります.各式の左辺の意味がわかっていれば,テンソル記号表記の右辺を導くのは簡単だと思います.また,クロネッカーのデルタやレヴィ・チヴィタ記号の公式も必要になりますので,ここに紹介しておきます.




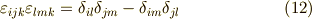
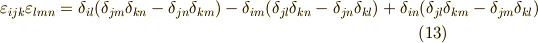
| [*] | この記事の内容と基本的に同じもので,より 本格的に解説した資料 を,愛媛大学元教授・矢野忠先生から御寄稿頂きましたので,ぜひ併せてご覧下さい.矢野先生,どうもありがとうございました. |
例題
例題として, よくある間違い で使った次の公式を導いてみましょう.
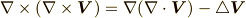
まず左辺をテンソル記号で表記します.ベクトル 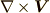 の第
の第 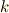 成分をテンソルでまず
成分をテンソルでまず 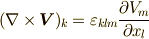 と書くところから始めましょう.添字は巡回的に
と書くところから始めましょう.添字は巡回的に 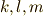 の順だとします.頑張って,もう一度
の順だとします.頑張って,もう一度 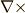 を作用させ,
を作用させ,  の第
の第 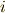 成分を表わします.添字は巡回的に
成分を表わします.添字は巡回的に 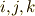 の順だとします.
の順だとします.
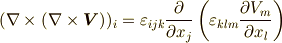
すでに頭がこんがらがっている人がいるかも知れませんが,式 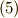 を使っただけです.添字が混ざらないようにすることだけに注意して下さい.以下,一行ごとにコメントと式変形を交互に書いていきます.まず
を使っただけです.添字が混ざらないようにすることだけに注意して下さい.以下,一行ごとにコメントと式変形を交互に書いていきます.まず 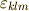 を外に出します.
を外に出します.
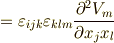
式 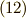 が使えるように,
が使えるように, 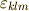 を
を 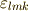 にします.
にします.  は偶置換なので符号は変わりません.
は偶置換なので符号は変わりません.
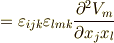
式 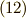 を使います.
を使います.
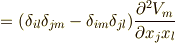
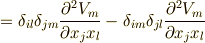
クロネッカーのデルタの作用を考えますが,出来る限り 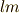 を消して
を消して 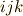 に統一する方向で整理します.
に統一する方向で整理します.
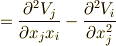
式 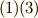 より第一項目は
より第一項目は 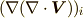 ,式
,式 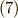 より第二項は
より第二項は 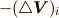 と書き直すことができます.公式が証明できました.
と書き直すことができます.公式が証明できました.