ベクトル場

まず，ある広がりを持った空間をイメージしてください．（日常用語の意味で連想する空間のイメージで結構です．）その空間内のどこでも一点で，それぞれ一つベクトルが定義されるとします．つまり，空間内の一点 $\bm{r}$ を指定すると， $\bm{r}$ の関数としてベクトルが一つ決まるということです．

$\bm{A} = \bm{A}(\bm{r}) \tag{1}$

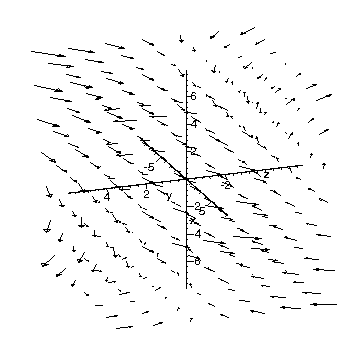
空間の各点で，場所の関数としてベクトルがひとつ決まる．こんなイメージか．

このような関数を ベクトル場 と呼びます．

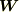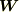例として分かりやすいのは，風でしょう．風には，風速（大きさ）と風向（向き）がありますからベクトルとして表現できます．そして，場所によって吹く向きも強さも違うのですから，．風ベクトルを $\bm{W}$ とすれば， $\bm{W}$ はベクトル場だと言えます．

$\bm{W} = \bm{W} (\bm{r}) \tag{2}$

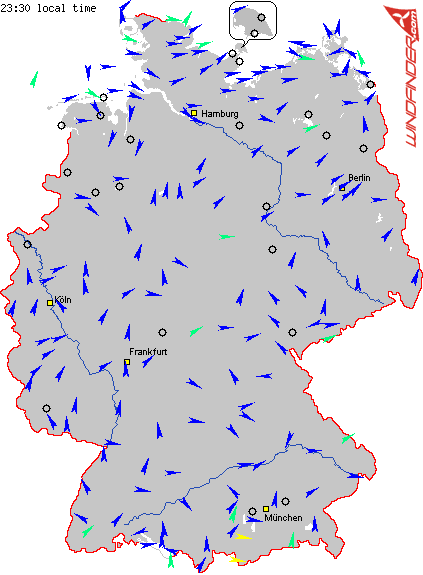
場所によって風は強さも向きも違う．ベクトル場だ．

風の例で分かるように，流れの研究をする流体力学ではベクトル場の考え方が非常に大事です．また，目に見える流れではありませんが，電場や磁場もベクトル場ですから，電磁気学でもベクトル場の考え方が大事です．実は，ベクトル解析という分野は，電磁気学の研究によって進歩してきたのです．力学とベクトル場については，最後のセクションで少し触れます．

[*]	本当は，風は時々刻々向きや大きさを変えますから，時間と場所の関数として 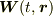$\bm{W}(t,\bm{r})$ と表わすほうが正確です．ベクトル場が時間の関数でもある場合は，しばらく考えませんが，この記事の最後のセクションで少しだけ触れます．

スカラー場

全く同様に，空間の各点に応じてスカラーが一つ決まる場合，この関数を スカラー場 と呼びます．

$\rho = \rho (\bm{r}) \tag{3}$

再び例を考えてみると，気圧や気温は空間内の場所に応じて決まるスカラーですから，スカラー場だと言えるでしょう．

テンソル場

空間内の一点 $\bm{r}$ に応じてテンソルが一つ決まるとき，このテンソルを $\bm{r}$ の関数とみて テンソル場 と呼びます．ベクトル場もスカラー場も，テンソル場の特別な場合です．

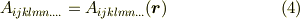
$A_{ijklmn....} = A_{ijklmn...}(\bm{r}) \tag{4}$

弾性体の内部の一点で決まる応力は，二次のテンソル場の例です．

ベクトル解析

ベクトル場（一般にはテンソル場）は，なにも空間内の各点で定義されるものばかりではなく，曲線に沿って曲線上の各点で定義されるベクトル場，曲面に沿って曲面上の各点で定義されるベクトル場などがあります．

ベクトル解析という分野は，狭い意味で言えばベクトル場の微積分を勉強する分野です．電場，磁場，流れ場，重力場，速度場などはベクトル場として表現できますので，物理学でも応用上とても大事な分野です．ベクトル解析の創始者はハミルトン( $\text{William Rowan Hamilton (1805-1865)}$ )やクリフォード( $\text{William Kingdon Clifford (1845-1879)}$ )といった数学者ですが，大いに発展させたのはヘヴィサンド( $\text{Oliver Heaviside (1850-1925)}$ )やギブス( $\text{Josiah Willard Gibbs (1839-1903)}$ )らで，マックスウェルの電磁気理論の研究がきっかけとなっています．

へヴィサイドは学校の勉強が嫌いで，特に厳密な数学は苦手だったそうですが，電信士として働き，モールス信号を打つ仕事の傍ら独学で少しずつ電磁気学の勉強を始めました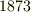． 1873 年，マックスウェルの論文 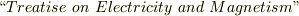$``Treatise \ on \ Electricity \ and \ Magnetism"$ に衝撃を受け，電信士をやめて研究に没頭することに決めたということです．マックスウェル方程式は当初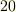個の変数からなる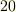本の方程式系からなっていましたが，ベクトル表記によって 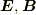$\bm{E},\bm{B}$ の二変数による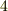本の方程式にまで簡単化したのはへヴィサイドの功績です．

ベクトル演算子の発明は生前から『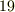世紀の三大発見』だと評価された．

エール大学で機械工学や数学を勉強したギブスも，やはりキルヒホッフやヘルムホルツの理論を通じて電磁気学への興味を深めていき，マックスウェルの電磁気理論がきっかけとなって，本格的にベクトル解析の研究を始めました．数学的にベクトル解析を洗練したのはギブスの功績で，グラスマン( 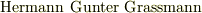$\text{Hermann Gunter Grassmann}$ )の研究成果を取り入れ，ハミルトンの四元数を使ったベクトル計算よりもずっと簡単な，今日私達が習うベクトル解析の基礎を打ち立てました．

アメリカ史上，最初の工学博士号はギブスに贈られた．

ベクトル解析は生まれたときから物理学との結びつきが非常に強かった分野であると言えるでしょう．

力学系への招待

少し発展的な内容になりますが，力学の文脈でベクトル場を考えてみましょう．古典的なニュートン力学の枠組みでは，物理状態の変化は微分方程式で表わされることになっています．つまり，物理状態の変化は連続的であるという仮定から出発します．

一般に，物理量を表わすベクトル 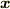$\bm{x}$ があったとして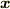， $\bm{x}$ の時間的変化は適当なベクトル値関数 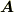$\bm{A}$ を使って次のように表わされるでしょう．

$\frac{d\bm{x}}{dt}=\bm{A}(\bm{x},t) \tag{5}$

つまり『物理量の変化は，その時その場所の系の状態によって決まる』という主張でもあります．特に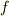が時間によらない場合，これを 自励系 と呼びます．

$\frac{d\bm{x}}{dt}=\bm{A}(\bm{x}) \tag{6}$

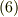式 (6) の右辺は，系の一点 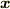$\bm{x}$ に対してベクトル値関数 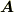$\bm{A}$ を対応させる形になっていますので，まさしくベクトル場です．式 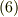(6) はベクトル場の時間変化を表わす微分方程式だと言えますが，このようなベクトル場を 力学系 と呼びます．

より一般には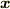， $\bm{x}$ は普通の意味の位置ベクトルには限定されません．適当な物理量からなる相空間内での位置ベクトルと考えて良いわけです．（位相空間参照．）また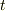も時間を意味するとは限りません．つまり，より一般には式 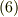(6) によって，問題になっている物理系の，あるパラメータに対する変動を調べることが出来るわけです．式 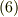(6) の微分方程式を積分して解くと，その解は相空間内の曲線として与えられますが，ここで (1) そもそも積分できるの？ (2) どんなとき積分できるの？ (3) 初期条件によって解はどう変わるの？といった疑問が噴出します．また，解は一つとは限りませんが，物理的に安定な状態を意味する解と，不安定ですぐに安定な状態に遷移してしまう状態を意味する解とがあり， (4) 解は安定なの？というようなことも気になってきます．

こんなことを調べる分野が力学系の理論です．カオスや複雑系という言葉を聞いたことがある人も多いと思いますが，これらも力学系の話です．ベクトル場からかなり話が脱線しました．力学系の理論で重要なのは，微分方程式の知識や可積分系の理論と呼ばれる分野の知識で，実はあまりベクトル解析に関係ないのですが，著者が面白そうだと思っているので，ベクトル場から発展して勝手に紹介させて貰いました（笑）．

[home] [ベクトル解析] [ページの先頭]