ベクトル場の流束と流管
ベクトル場 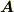 の中に,流れを横切るように適当に曲面
の中に,流れを横切るように適当に曲面 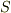 を取ります.曲面
を取ります.曲面 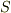 の面積素を
の面積素を 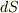 ,そこでの法線ベクトルを
,そこでの法線ベクトルを 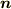 とするとき,式
とするとき,式 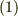 の形の量を考えます.
の形の量を考えます.

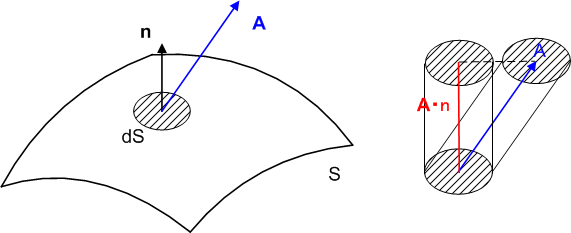
式  で表わされる量の物理的意味は明快です.上右図に示すように,
で表わされる量の物理的意味は明快です.上右図に示すように, 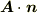 は,ベクトル場
は,ベクトル場 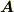 を
を 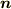 方向に射影した長さ(図赤線)ですので,『底面
方向に射影した長さ(図赤線)ですので,『底面  高さ』で
高さ』で 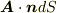 は図の円柱の体積を表わしていることになります.このベクトル場が流れの流速を表わしているならば,
は図の円柱の体積を表わしていることになります.このベクトル場が流れの流速を表わしているならば, 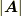 は単位時間当たりに流体が進む距離ですから,
は単位時間当たりに流体が進む距離ですから, 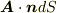 は 単位時間当たりにdSを通過する流体の流量を表わしている と考えることが出来ます.まず,ここまで流し読みしないでしっかり理解して下さい.
は 単位時間当たりにdSを通過する流体の流量を表わしている と考えることが出来ます.まず,ここまで流し読みしないでしっかり理解して下さい.
式 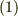 の量を曲面
の量を曲面 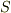 全体に渡って積分した量は,
全体に渡って積分した量は, 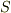 を単位時間当たりに通過する総流量になります.これを 流束 と呼び,記号には
を単位時間当たりに通過する総流量になります.これを 流束 と呼び,記号には 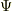 をよく用います.
をよく用います.
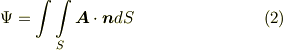
また,単位時間当たりに 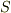 を通過する流体の質量
を通過する流体の質量 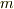 は,流体の密度
は,流体の密度 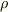 を掛けて次のように表わせます.(流体が非圧縮流体ならば,密度は定数ですので積分記号の外に出せます.)
を掛けて次のように表わせます.(流体が非圧縮流体ならば,密度は定数ですので積分記号の外に出せます.)
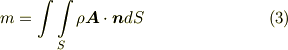
| [*] | 流体が増えたり減ったりしないならば,全体の流量は変わらないはずですから,流れの断面積が大きくなれば,その分流れは緩く,逆に流れの断面積が小さくなれば,その分流れは速くなります.(ホースの先をつまむと水が勢い良くなることを思い出してください.)一方,流線は途中で増えたり減ったりしませんから,流れの断面積が広がれば流線の密度は薄く,流れの断面積が小さくなれば流線の密度は高くなります.このため,流線の密度と流量は比例していると考えることができます.この見方に立てば,『流速とは流線の数である』とも言えます.もっとも,何本と言うには,流量と流線数の比を最初に決めておかなければなりません. |
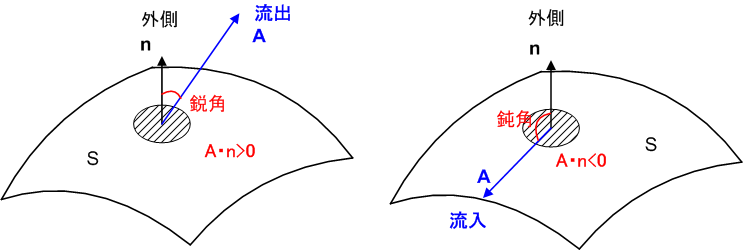
曲面 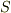 が表と裏を区別できる曲面であるとするとき,例えば
が表と裏を区別できる曲面であるとするとき,例えば 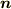 の正方向を曲面の外側に向かう向き(流れが出て行く向き)と決めることが出来ます.このとき,
の正方向を曲面の外側に向かう向き(流れが出て行く向き)と決めることが出来ます.このとき, 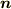 と
と 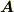 のなす角が鋭角ならば
のなす角が鋭角ならば 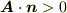 ,
, 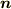 と
と 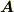 のなす角が鈍角ならば
のなす角が鈍角ならば 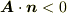 が言えますから,
が言えますから, 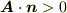 は
は 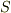 を通って外に出て行く流れ,
を通って外に出て行く流れ, 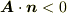 は
は  から流入する流れを表わすことになります.
から流入する流れを表わすことになります.
また, 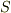 が閉曲面のとき,
が閉曲面のとき, 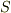 全面を通過する正味の流量を考えることで,
全面を通過する正味の流量を考えることで, 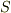 によって囲まれる領域の内部で発生したり消滅したりする流れの総量を知ることが出来ます.この考え方が ガウスの発散定理 と呼ばれる定理になりますので,この後も大事です.
によって囲まれる領域の内部で発生したり消滅したりする流れの総量を知ることが出来ます.この考え方が ガウスの発散定理 と呼ばれる定理になりますので,この後も大事です.
ベクトル場が電場や磁場の場合には,目では見えない流れになりますが,基本的なイメージは同じです.(この場合,流束は 電束 , 磁束 などと呼ばれます.)例えば,電束は次式で与えられます.式  と形はまるきり一緒ですね.
と形はまるきり一緒ですね.
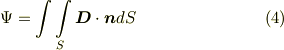
ここに出て来る 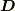 を 電束密度 と呼びます.いい加減に考えれば,電束密度とは単位面積当たりの電束と言っても良いでしょう.しかし,流束が『単位時間当たりに曲面
を 電束密度 と呼びます.いい加減に考えれば,電束密度とは単位面積当たりの電束と言っても良いでしょう.しかし,流束が『単位時間当たりに曲面 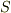 を通過する流量』という意味だったことを思い出すと,曲面
を通過する流量』という意味だったことを思い出すと,曲面 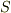 の取り方(つまり
の取り方(つまり 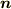 と
と 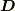 のなす角)によって
のなす角)によって 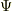 は変わって来ます.この意味で,電束密度を単に『電束÷面積』だと思ってしまっては早計です. 曲面の向きも重要なのだ という点を肝に銘じておいて下さい.(ただし
は変わって来ます.この意味で,電束密度を単に『電束÷面積』だと思ってしまっては早計です. 曲面の向きも重要なのだ という点を肝に銘じておいて下さい.(ただし 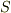 が閉曲面の場合,いずれにせよ流れには逃げ場が無いですから,流束は全流量に等しくなります.)ここでは,電磁気学の知識を前提にせず,似たような式や概念が出て来る例として電束や電束密度に少し触れましたが,より詳しくは こちら を参照して下さい.
が閉曲面の場合,いずれにせよ流れには逃げ場が無いですから,流束は全流量に等しくなります.)ここでは,電磁気学の知識を前提にせず,似たような式や概念が出て来る例として電束や電束密度に少し触れましたが,より詳しくは こちら を参照して下さい.
流管
連続なベクトル場 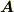 の中に,流れを横切るように適当に曲面
の中に,流れを横切るように適当に曲面 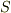 を取ります.また,
を取ります.また, 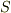 上の各点では
上の各点では 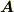 の流線が定義されます.このとき,
の流線が定義されます.このとき, 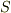 を通る
を通る 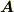 の流線を全て集めてたばねたものを 流管 と呼びます.
の流線を全て集めてたばねたものを 流管 と呼びます.
流線を全部集めると,なんだか管のような形になるだろう.
図は, 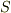 上の領域
上の領域 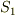 を通る流管です.流管の側面の部分は流線に沿っていますので,流管に沿って流れ場を考えた場合,流管の内部に湧き出しや吸い込みの無い流れであれば,どんなに流管が広がったり細くなったりしようと, 流管の側面を出入りする流れはありません ので,流管の断面を通過する流量はいつでも等しいことが言えます.つまり,流管が他の任意の平面を切る断面を
を通る流管です.流管の側面の部分は流線に沿っていますので,流管に沿って流れ場を考えた場合,流管の内部に湧き出しや吸い込みの無い流れであれば,どんなに流管が広がったり細くなったりしようと, 流管の側面を出入りする流れはありません ので,流管の断面を通過する流量はいつでも等しいことが言えます.つまり,流管が他の任意の平面を切る断面を 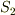 とすれば,
とすれば, 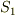 と
と 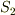 について常に次式がなりたちます.
について常に次式がなりたちます.
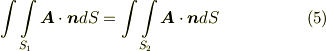
流管の考え方も,流体力学や電磁気学で大切になってきます.特に,至るところ 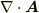 がなりたつベクトル場を 管状ベクトル場 と呼びますが,管状ベクトル場はまさに,上図のように管を流れるイメージです.式
がなりたつベクトル場を 管状ベクトル場 と呼びますが,管状ベクトル場はまさに,上図のように管を流れるイメージです.式 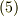 は管状ベクトル場にとって非常に重要な式です.また,式
は管状ベクトル場にとって非常に重要な式です.また,式 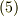 により,流管はどこで切っても断面を通る流量が一定だというのですから,湧き出しや吸い込みがない限りは,流管が出現したり消えたりということは無いはずです.そこで,次の性質が言えます.
により,流管はどこで切っても断面を通る流量が一定だというのですから,湧き出しや吸い込みがない限りは,流管が出現したり消えたりということは無いはずです.そこで,次の性質が言えます.
theorem
湧き出し・吸い込みの無い流れ(管状ベクトル場)では,流管は消えたり生まれたりしません.
この定理より,湧き出し・吸い込みの無い流れにおける流管は,次のタイプのいずれかに分類されることになります.
- 流管は無限に長い.(定義域が無限の場合)
- グルッと輪になって閉じている.
- 定義域の境界で終わる.(定義域が有限の場合)
二番目の場合については,領域の形に注意が必要です.詳しくは ポテンシャルと流線 を参照して下さい.