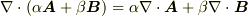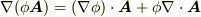div
スカラー場の勾配を考えたとき,ベクトル微分演算子 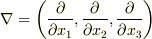 というものを導入しました.そして,この
というものを導入しました.そして,この 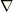 をスカラー関数に作用させたものを勾配(
をスカラー関数に作用させたものを勾配(  )と呼びました.
)と呼びました. 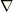 をベクトル関数と内積を取る形で作用させたものを 発散 と呼びます.英語で発散を
をベクトル関数と内積を取る形で作用させたものを 発散 と呼びます.英語で発散を  と言うので,記号
と言うので,記号 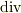 を使う場合もあります.
を使う場合もあります.
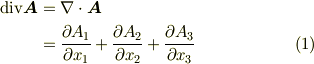
ただし,式中  としました.単に
としました.単に  とベクトルの内積になっているだけなので,計算が特に難しいということは無いと思います.
とベクトルの内積になっているだけなので,計算が特に難しいということは無いと思います.
発散のイメージ
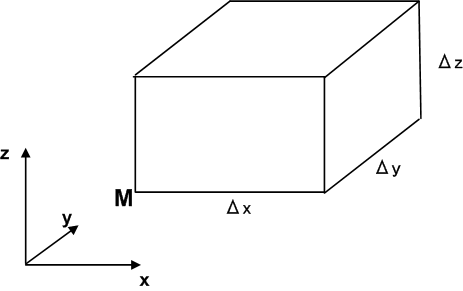
ここでは,デカルト座標系を考えます.ベクトル場が,点  において
において  と表現されるとき,
と表現されるとき,  を一つの頂点に,各辺の長さが
を一つの頂点に,各辺の長さが 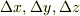 の直方体領域を考えます.
の直方体領域を考えます.
ベクトル場を,水(非圧縮流体)の流れだと考えると状況がイメージしやすいでしょう.この直方体領域は流れの中に置かれていますから,絶えず水が流れ込んだり出て行ったりしています.しかし,水は非圧縮流体だと仮定していますので,普通なら,入ってくる水量と出て行く水量は同じはずです.ところが,もしこの領域内に"温泉の湧き出し口"のように,絶えず水を噴出している穴が空いているとすればどうでしょうか?全体で,出て行く水の方が多くなりそうですね.逆に,水を吸い込んでしまう排水口のような穴が空いているとしたら,流入する水量の方が多くなりそうです.こうした点を 湧き出し , 吸い込み と呼びます.
| [*] | 湧き出し口や排水口に水道パイプはつながっているのか?などと,現実的なことを考えてはいけません.数学的に,空間のある一点が(上下水道なしでいきなり)水を噴出したり吸い込んだりしていると仮定しての話です.宇宙のどこかには,ブラックホールやホワイトホールと呼ばれる,湧き出しや吸い込みがあるようですが,そんなイメージでお願いします. |
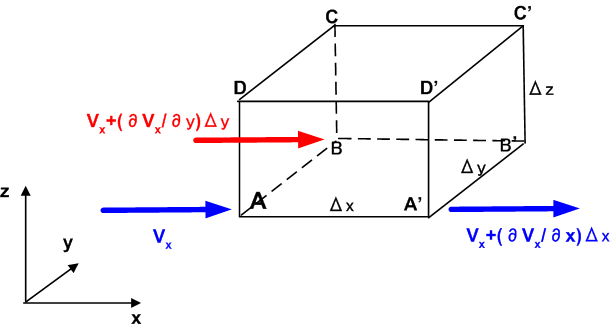
例として,  軸方向に流入する量と流出する量の差を考えてみます.図のように,頂点
軸方向に流入する量と流出する量の差を考えてみます.図のように,頂点 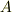 付近に単位面積当たり流入する流体の量は
付近に単位面積当たり流入する流体の量は 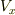 で表わされ,頂点
で表わされ,頂点 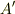 付近では
付近では 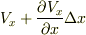 と表わされます.その差は
と表わされます.その差は  です.
です.
ここまでは偏微分を定義通りに使っただけです.面倒なのは,正確に表現しようとすると『  方向への変化』されも,
方向への変化』されも,  軸や
軸や  軸に沿って変化することです.つまり,頂点
軸に沿って変化することです.つまり,頂点 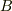 付近で
付近で  方向の流入流は
方向の流入流は  と表現され,さらに
と表現され,さらに  付近ではこの値の
付近ではこの値の  方向への変化を考え,流出流は次式のように表現されることになります.(ここで図に全て書き込むとごちゃごちゃしますので描きませんでした.大事なところですので,自分で似たような図でも描いて,しっかり考えてみて下さい.)
方向への変化を考え,流出流は次式のように表現されることになります.(ここで図に全て書き込むとごちゃごちゃしますので描きませんでした.大事なところですので,自分で似たような図でも描いて,しっかり考えてみて下さい.)
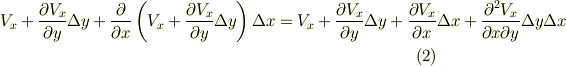
ここで,直方体領域は十分に小さいとすれば,  方向の流れは "ほぼ一様"だと考えて,二次の変化量(右辺第三項)を無視できます.結局,頂点
方向の流れは "ほぼ一様"だと考えて,二次の変化量(右辺第三項)を無視できます.結局,頂点 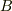 付近での流量の差は
付近での流量の差は 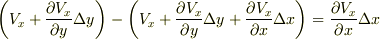 と近似できることになります.これは頂点
と近似できることになります.これは頂点 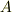 付近の流れと同じになります.
付近の流れと同じになります.  方向に関しても同様に
方向に関しても同様に 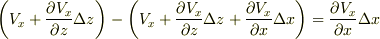 が言えますから,結局,面
が言えますから,結局,面 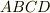 に流入する流体と,面
に流入する流体と,面 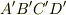 から流出する流体の差は,単位面積あたり
から流出する流体の差は,単位面積あたり  と書いてしまって良いことになります.
と書いてしまって良いことになります.
Important
微小直方体領域で,  軸方向に『
軸方向に『 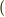 流出した量
流出した量  流入した量
流入した量 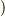 』を,
』を, 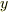 軸方向や
軸方向や  軸方向への二次的な変化を無視すると,単位面積あたり
軸方向への二次的な変化を無視すると,単位面積あたり  と表わせる
と表わせる
ここで  軸方向の流れだけを考えて『
軸方向の流れだけを考えて『 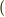 流出した量
流出した量  流入した量
流入した量 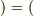 内部で湧き出した量
内部で湧き出した量 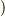 』と考えてしまっては早計です.
』と考えてしまっては早計です.  軸方向や
軸方向や  軸方向からの流体の出入りも考慮しなければならないからです.しかし,もし全方向で『
軸方向からの流体の出入りも考慮しなければならないからです.しかし,もし全方向で『 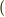 流出した量
流出した量  流入した量
流入した量 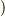 』を考えれば,これは『
』を考えれば,これは『 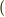 内部で湧き出した量
内部で湧き出した量 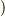 』に等しくなります.
』に等しくなります.
この直方体の  軸方向の断面積(上図の四角形
軸方向の断面積(上図の四角形 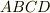 の面積)が
の面積)が 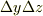 であることに注意すると,
であることに注意すると,  軸方向の流量の差
軸方向の流量の差 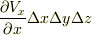 と表わされます.同様に,
と表わされます.同様に, 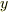 軸方向の流量の差は
軸方向の流量の差は 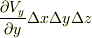 ,
, 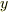 軸方向の流量の差は
軸方向の流量の差は 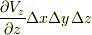 となり,この直方体全体から流出する流量はこれらを足して次式になります.
となり,この直方体全体から流出する流量はこれらを足して次式になります.
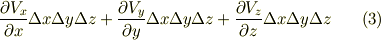
最後に,これを直方体の体積 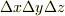 で割れば, 単位体積当たりの湧き出し量 の表式を得ます.これは,もうお気づきのように
で割れば, 単位体積当たりの湧き出し量 の表式を得ます.これは,もうお気づきのように 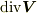 になっています.
になっています.
Important
単位体積当たりの湧き出しは  で表わされます.
で表わされます.
ベクトル場 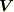 が水の流れ以外のベクトル場であっても,流れの物理的意味は少し異なるかも知れませんが,基本的には『単位体積当たりの流れの増減』を表わすのが発散だと考えることができます.このようなイメージを持っていれば,電磁気学で電場や磁場といった目に見えない場の計算に
が水の流れ以外のベクトル場であっても,流れの物理的意味は少し異なるかも知れませんが,基本的には『単位体積当たりの流れの増減』を表わすのが発散だと考えることができます.このようなイメージを持っていれば,電磁気学で電場や磁場といった目に見えない場の計算に  が出てきても,慌てることは無いと思います.
が出てきても,慌てることは無いと思います.
また, ベクトル解析奮闘記2 では,以上の議論が直観的に分かりやすい絵と,味のある文で学習者の視点から説明されています.ぜひ,そちらも参照してください!
| [†] | 発散の意味の物理的意味は分かったでしょうか.流体力学で,湧き出しや吸い込みの無い非圧縮流体の流れは, 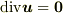 と表現されることになります.この式を見て,『非圧縮流で,湧き出しの無い流れだな』とすぐに読めるくらいになると素敵です. と表現されることになります.この式を見て,『非圧縮流で,湧き出しの無い流れだな』とすぐに読めるくらいになると素敵です. |
発散の演算規則
発散をとる操作も線形演算ですので,以下のような算法がなりたちます.発散も線形ですね.
歴史
ベクトルは 四元数 から発生したものですが,四元数の基底 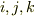 を使ったベクトルの積は次式のようになります.(詳しくは 七次元の外積 を参照下さい.)
を使ったベクトルの積は次式のようになります.(詳しくは 七次元の外積 を参照下さい.)
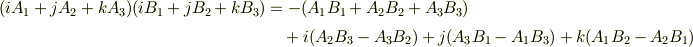
この右辺第一項は,私達が知っている内積にマイナスがついた形をしています.ベクトル解析が生まれた頃は,どうしてもこの四元数の乗法が念頭にあったためか,内積にマイナスをつける流儀の人が多く,例えば電磁気学のマックスウェル(  )は,四元数の基底を使って
)は,四元数の基底を使って  という記号を使っていました.この記号をベクトル
という記号を使っていました.この記号をベクトル 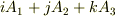 に作用させたときのスカラー項を
に作用させたときのスカラー項を 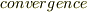 と呼び,当時は
と呼び,当時は 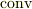 などと書いていました.
などと書いていました.

これは,ちょうど私達がいま使っている発散 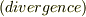 と符号が逆ですから,物理的には吸い込みを意味することになります.
と符号が逆ですから,物理的には吸い込みを意味することになります. 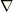 を現在の形にし,ずっと扱い易くしたのはヘヴィサイド(
を現在の形にし,ずっと扱い易くしたのはヘヴィサイド(  )の功績です.現在では
)の功績です.現在では 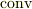 なんて使う人は誰もいませんし,ベクトル解析の表記はとてもすっきりと自然な形にまとまっています.数学の進歩のためには美しい表記法が重要だというのは,微積分の記号を発明したライプニッツ(
なんて使う人は誰もいませんし,ベクトル解析の表記はとてもすっきりと自然な形にまとまっています.数学の進歩のためには美しい表記法が重要だというのは,微積分の記号を発明したライプニッツ(  )の信念だったそうですが,
)の信念だったそうですが, 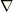 や後述する
や後述する  などは確かによく出来た記号で,こうした記号のお陰で,ベクトル解析の公式の中には芸術的とも言える美しいものがあるのです.
などは確かによく出来た記号で,こうした記号のお陰で,ベクトル解析の公式の中には芸術的とも言える美しいものがあるのです.