ベクトル成分の座標変換

まず 基底の座標変換 の記事で見た，双対基底の座標変換を思い出しましょう．双対基底は変換係数 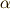{\alpha} を使って次のように表現できるのでした．

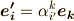
\bm{e'_{i}}= {\alpha}_{i'}^{k}\bm{e_{k}}
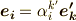
\bm{e_{i}}= {\alpha}_{i}^{k'}\bm{e'_{k}}

双対基底の性質 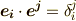\bm{e_{i}} \cdot \bm{e^{j}} ={\delta}_{i}^{j} を使えば，係数 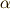{\alpha} は次のように基底の内積によって表現できます．

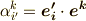
{\alpha}_{i'}^{k} = \bm{e'_{i}} \cdot \bm{e^{k}}
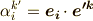
{\alpha}_{i}^{k'} = \bm{e_{i}} \cdot \bm{e'^{k}}

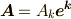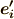そこで，ベクトル \bm{A}=A_{k} \bm{e^{k}} の両辺に \bm{e'_{i}} を乗じると次式を得ます．

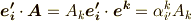
\bm{e'_{i}} \cdot \bm{A}=A_{k} \bm{e'_{i}} \cdot \bm{e^{k}} = {\alpha}_{i'}^{k} A_{k}

左辺は \bm{e'_{i}} \cdot \bm{A}=\bm{e'_{i}} \cdot (A'_{j} \bm{e'^{j}})={\delta}_{i'}^{j'}A'_{j}=A'_{i} と書けますので，結局，次の関係式が得られます．

A'_{i}= {\alpha}_{i'}^{k} A_{k} \tag{1}

これは共変ベクトル（反変基底をとったときの成分）の座標変換の式です．全く同様にして，反変ベクトル（共変基底を取ったときの成分）の座標変換も次のように表わされます．

A'^{i}= {\alpha}_{k}^{i'} A^{k} \tag{2}

ベクトル成分の座標変換も，基底と同じ変換係数を使って表現することができました．式 (1)(2) は，ベクトル成分の座標変換を表わす一般式になっています．添字の上下と，ダッシュの付いている位置にもよく注意してください．式 (1)(2) を行列の形で書くこともできます．

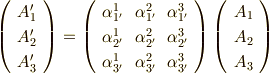
\left( \begin{array}{ccc} A'_{1}\\ A'_{2}\\ A'_{3}\\ \end{array} \right) =\left( \begin{array}{ccc}{\alpha}_{1'}^{1} & {\alpha}_{1'}^{2} & {\alpha}_{1'}^{3} \\{\alpha}_{2'}^{1} & {\alpha}_{2'}^{2} & {\alpha}_{2'}^{3} \\{\alpha}_{3'}^{1} & {\alpha}_{3'}^{2} & {\alpha}_{3'}^{3} \\\end{array}\right) \left( \begin{array}{ccc} A_{1}\\ A_{2}\\ A_{3}\\ \end{array} \right)
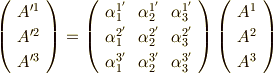
\left( \begin{array}{ccc} A'^{1}\\ A'^{2}\\ A'^{3}\\ \end{array} \right) =\left( \begin{array}{ccc}{\alpha}_{1}^{1'} & {\alpha}_{2}^{1'} & {\alpha}_{3}^{1'} \\{\alpha}_{1}^{2'} & {\alpha}_{2}^{2'} & {\alpha}_{3}^{2'} \\{\alpha}_{1}^{3'} & {\alpha}_{2}^{3'} & {\alpha}_{3}^{3'} \\\end{array}\right) \left( \begin{array}{ccc} A^{1}\\ A^{2}\\ A^{3}\\ \end{array} \right)
[*]ここに出てくる変換係数 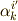{\alpha}_{k}^{i'} は，実は二階のテンソルと呼ばれるものです．テンソルはもうすぐ勉強しますので，何となく名前だけでも頭の片隅に置いておいて下さい．
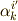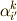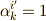[†]変換係数 {\alpha}_{k}^{i'} と {\alpha}_{i'}^{k} は逆変換の関係になっています．また変換を連続して行うことも出来ますし，もしも {\alpha}_{k}^{i'}=1 ならばこれは恒等変換となりますので，変換係数の集合は群をなします．( 群の公理 参照．) この群を，中心化アフィン群と呼びます．中心化アフィン群は，ベクトルの長さを変えない変換ですが，直交座標系以外の基底を含みますので色々な基底ベクトルの取り方に対応した幅広い変換を表現できます．鏡像変換，反変変換などの直交変換や，回転変換もそれぞれ群を作りますが，全て中心化アフィン群の部分群と考えることができます．