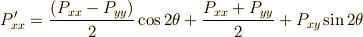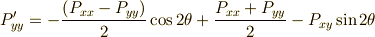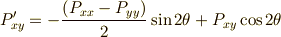二階のテンソルの回転変換
この記事では,座標系を角 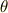 だけ回転させたとき,二階のテンソルの表現がどう変わるかを考察します.簡単のため二次元で考えることにし,座標系
だけ回転させたとき,二階のテンソルの表現がどう変わるかを考察します.簡単のため二次元で考えることにし,座標系 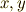 を角
を角 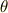 だけ回転させたものを座標系
だけ回転させたものを座標系 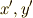 とします.
とします.
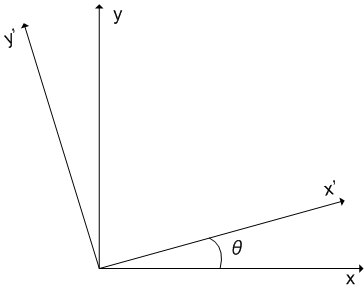
このとき,座標成分の変換は次式に従います.
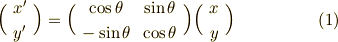
最初の予告しておきますが,一階のテンソルであるベクトルは式 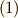 のような単純な変換式に従いましたが,二階のテンソルの変換式はもっとずっと複雑になります.(式
のような単純な変換式に従いましたが,二階のテンソルの変換式はもっとずっと複雑になります.(式 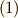 を,一階のテンソルを二階のテンソルによって座標変換していると見ることができます.二階のテンソルを同様に変換するには,四階のテンソルが必要です.)行列や
を,一階のテンソルを二階のテンソルによって座標変換していると見ることができます.二階のテンソルを同様に変換するには,四階のテンソルが必要です.)行列や  を大量に使うのは骨が折れるので,式
を大量に使うのは骨が折れるので,式 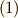 の代わりに複素数を使った回転変換を利用することにします.
の代わりに複素数を使った回転変換を利用することにします.
| [*] | 物理学で応用上,座標を回転変換させる場合に,二階のテンソルの成分の変換式を求めるのは重要です.慣性モーメントや応力-ひずみテンソルの計算に習熟する必要がある人にとって,この記事の内容は大事だと思います.このような計算が応用上あまり必要ではない人にも『二階のテンソルの座標変換って,ベクトルの座標変換より大変なんだなぁ.』ということだけでも感じて頂けたらと思います. |
複素数を使った回転の表現
複素数を使って,式 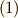 と同じ変換を次のように表わすことにします.
と同じ変換を次のように表わすことにします.
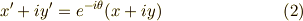
見ただけでピンと来ない人は,まず,式  を実部と虚部に分ければ式
を実部と虚部に分ければ式 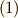 と同じ変換式になることを確認して下さい.式
と同じ変換式になることを確認して下さい.式  の複素共役を取れば次式となります.
の複素共役を取れば次式となります.
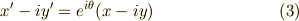
式 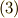 と式
と式  は,どちらも式
は,どちらも式 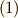 と同じ変換式を表わしています.この後,ベクトル成分
と同じ変換式を表わしています.この後,ベクトル成分 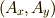 の回転変換を考えますが,式
の回転変換を考えますが,式 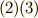 を利用したいので,計算中は常に
を利用したいので,計算中は常に  か
か 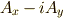 の形を使うことにします.これを簡単に次のように表記することにします.
の形を使うことにします.これを簡単に次のように表記することにします.
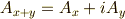
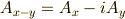
この表記を用いると,式 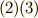 は次のように簡単にまとめられます.
は次のように簡単にまとめられます. 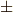 の符号に注意してください.
の符号に注意してください.

さて,式 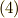 と同じ変換に従うベクトル
と同じ変換に従うベクトル 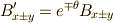 をもう一つ考え,
をもう一つ考え, 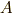 と
と 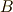 の積を考えます.ただし,
の積を考えます.ただし, 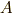 と
と 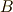 で
で 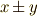 の符号が別々になる可能性があるので,
の符号が別々になる可能性があるので, 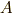 の符号を
の符号を 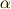 (
( 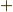 か
か  ),
), 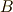 の符号を
の符号を  (
( 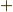 か
か  )として,次のように書きましょう.
)として,次のように書きましょう.
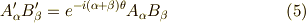
ここまではベクトルの回転変換の話でした.式 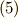 から,幾つかの事柄を整理できます.
から,幾つかの事柄を整理できます. 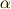 と
と  の組み合わせが
の組み合わせが 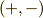 もしくは
もしくは 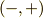 の場合,
の場合, 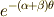 の部分が消えますから, 式
の部分が消えますから, 式 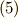 はある種の不変量を表わす式になります.
はある種の不変量を表わす式になります.

実際に,式  を実部と虚部に分けると次式を得ます.(符号の組み合わせとして
を実部と虚部に分けると次式を得ます.(符号の組み合わせとして 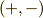 でも
でも 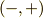 でも同じ式が得られます.)最初の式は内積が不変であること,二番目の式は外積の
でも同じ式が得られます.)最初の式は内積が不変であること,二番目の式は外積の  成分が不変であること(
成分が不変であること( 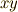 平面内の回転を考えているので当然ですね)を表わしています.
平面内の回転を考えているので当然ですね)を表わしています.
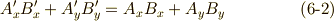
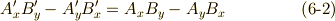
さて,テンソルの議論に使うため,式  の符号について,全ての場合を場合分けしておくことにします.ここまで複素ベクトルの添字を
の符号について,全ての場合を場合分けしておくことにします.ここまで複素ベクトルの添字を 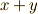 のように書いていましたが,面倒なので次のように真ん中の符号だけで略記することにします.また,
のように書いていましたが,面倒なので次のように真ん中の符号だけで略記することにします.また, 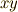 平面内の回転とは関係のない
平面内の回転とは関係のない  成分を,
成分を,  として仲間に加えることにします.
として仲間に加えることにします.
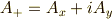

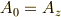
この略記法を使って,積 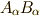 を場合分けすると,次のようになります.
を場合分けすると,次のようになります.

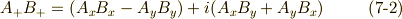
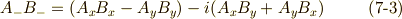
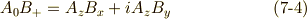
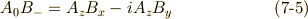
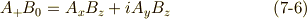

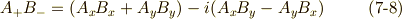
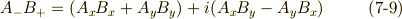
二階のテンソルの変換式
さきほど複素ベクトルの積の変換式を場合分けしましたが, 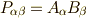 と置くことで,これをそのまま二階のテンソルの変換式に置き換えることができます.( ベクトルからテンソルを作る 参照.)式
と置くことで,これをそのまま二階のテンソルの変換式に置き換えることができます.( ベクトルからテンソルを作る 参照.)式 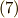 をそのまま
をそのまま 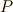 に置き換えて,次式を得ます.
に置き換えて,次式を得ます.

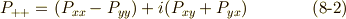
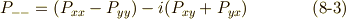






さらに,個々の成分(  ,
, 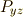 等々)は,座標の変換式
等々)は,座標の変換式 ![P'_{\alpha \beta}=e^{-(\alpha +\beta )\theta }P_{\alpha \beta }=[\cos (\alpha +\beta )\theta -i\sin (\alpha +\beta )]P_{\alpha \beta }](./5bd1f02b8eae6bbc57cc3c8c8ec4ccfd.png) に従いますので,これを左辺に代入し,実部と虚部をそれぞれ比較することで以下の式
に従いますので,これを左辺に代入し,実部と虚部をそれぞれ比較することで以下の式 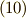 を得ます.(
を得ます.( 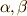 は
は 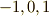 のどれかとします.)
のどれかとします.) 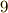 本の式から実部と虚部で
本の式から実部と虚部で 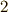 本ずつ式が出てくるので,合計
本ずつ式が出てくるので,合計 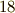 本の式になりそうですが,同じものが
本の式になりそうですが,同じものが 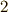 本ずつ出てくるので,実際は次の
本ずつ出てくるので,実際は次の 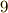 本の式になることに注意して下さい.
本の式になることに注意して下さい.

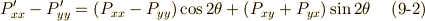
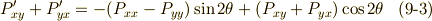

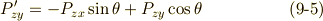
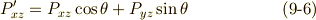
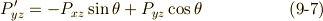

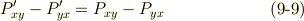
これらを連立して, 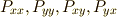 の変換式は次のように求まります.
の変換式は次のように求まります.
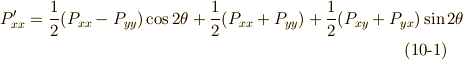
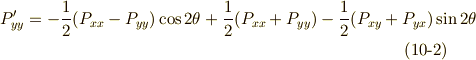
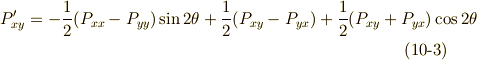
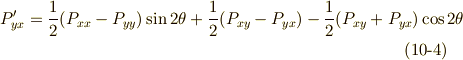
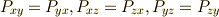 がなりたちます.剛体の力学や連続体力学で対称テンソルは特に重要だと思いますが,式
がなりたちます.剛体の力学や連続体力学で対称テンソルは特に重要だと思いますが,式 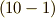 〜
〜  に,
に,