テンソルの主軸2
ここまでに勉強したことを復習しておきます. テンソルの主軸1 では二階のテンソルの 固有値 , 固有ベクトル , 主方向 (固有ベクトルの方向)という概念を勉強しました.二階のテンソル 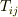 の固有値
の固有値 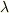 と固有ベクトル
と固有ベクトル 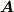 は次式を満たすものとして定義されます.
は次式を満たすものとして定義されます.

ただし,座標系は正規直交座標系を考えています.式 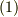 で
で 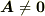 とすると行列式
とすると行列式  に至りますが,これを 固有方程式 と呼びます.重解が無い場合には三次方程式となるので三つの固有値が決まり,それぞれの固有値に対して固有ベクトルと主方向が一つずつ決まります.
に至りますが,これを 固有方程式 と呼びます.重解が無い場合には三次方程式となるので三つの固有値が決まり,それぞれの固有値に対して固有ベクトルと主方向が一つずつ決まります.
この記事では,固有ベクトルや主方向についてもう少し考察を深めたいと思います.
対称テンソルの固有ベクトルは直交する
二階の対称テンソル 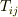 を考えます.
を考えます.

まず, 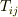 の相異なる二つの固有値を
の相異なる二つの固有値を 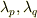 と置き,それぞれに対応する固有ベクトルを
と置き,それぞれに対応する固有ベクトルを 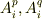 と書きます.
と書きます.  定義より,式
定義より,式 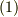 が満たされるはずです.
が満たされるはずです.


式  の両辺に
の両辺に 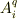 ,式
,式 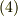 の両辺に
の両辺に 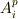 を乗じ,辺々引きます.
を乗じ,辺々引きます.
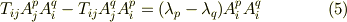
ここで,左辺は式 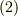 より零となりますが,右辺では
より零となりますが,右辺では 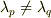 を仮定していましたから,
を仮定していましたから, 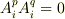 が要請されます.これは
が要請されます.これは 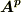 と
と 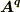 の内積が零になるということで,固有ベクトルが直交していることを意味しています.
の内積が零になるということで,固有ベクトルが直交していることを意味しています.
Important
対称テンソルの固有ベクトルは直交します.
テンソルの主軸変換
対称テンソルの主方向は互いに直交することが分かりましたので,直交座標系をテンソルの主方向に合わせて取れば,テンソルの作用が非常に見やすくなることが予想されます.座標系をテンソルの主方向に取れば,このテンソルをベクトルに作用させる場合に,ベクトルの各成分を固有値倍すれば良いだけとなるのですね.いま考えているテンソルは二階のテンソルですから,操作自体は,線形代数で勉強した『行列の対角化』と同じことです.
最初に考えた 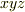 座標系でテンソルが
座標系でテンソルが 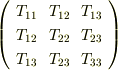 と表現され,ある適当なベクトル
と表現され,ある適当なベクトル 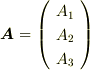 に作用する場合を考えましょう.
に作用する場合を考えましょう. 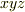 座標系をテンソルの主軸座標系に座標変換することで,同じ作用を表現するにも,テンソルの表現行列は対角化されます.もちろん,この座標変換に伴って,
座標系をテンソルの主軸座標系に座標変換することで,同じ作用を表現するにも,テンソルの表現行列は対角化されます.もちろん,この座標変換に伴って, 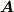 の成分も変わるので,適当に
の成分も変わるので,適当に 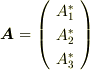 と書いておきます.
と書いておきます.
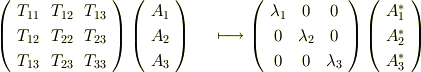
このような座標変換を, 主軸変換 と呼びます.テンソルは,主方向に沿ってベクトルの成分を定数倍するように働いており,その定数が固有値なのだと考えられます.テンソルのこのような働きが一番よく見えるのが,主方向に沿った座標系の取り方だということです.そして対称テンソルの場合には直交座標系を取れるわけです.
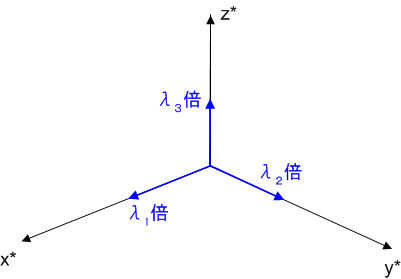
図にうまく書けませんでしたが,固有値が分数や負数なら,縮小や反転になります.
固有方程式が重解を持つ場合
ここまで,固有方程式が重解を持たず, 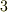 つの相異なる固有値があることを前提に議論してきました.では,固有方程式が重解を持つ場合,固有ベクトルや主方向はどうなるのでしょうか?
つの相異なる固有値があることを前提に議論してきました.では,固有方程式が重解を持つ場合,固有ベクトルや主方向はどうなるのでしょうか?
実際に計算してみればすぐに確認できることですが,固有値の大きさには関係なく,対称テンソルは 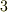 つの互いに直交する固有方向を持ちます.たまたま,大きさが同じであっただけで,固有ベクトルの向きは,ちゃんと別に取れるのですね.
つの互いに直交する固有方向を持ちます.たまたま,大きさが同じであっただけで,固有ベクトルの向きは,ちゃんと別に取れるのですね.
少し面倒なのは,固有値方程式が二次方程式に縮退してしまう場合(もしくは零が解に含まれる場合)です.このとき,  つの固有値のうちの一つが
つの固有値のうちの一つが 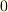 なのだという言い方もできますが,これによってベクトルはどのような変換を受けるでしょうか.
なのだという言い方もできますが,これによってベクトルはどのような変換を受けるでしょうか.
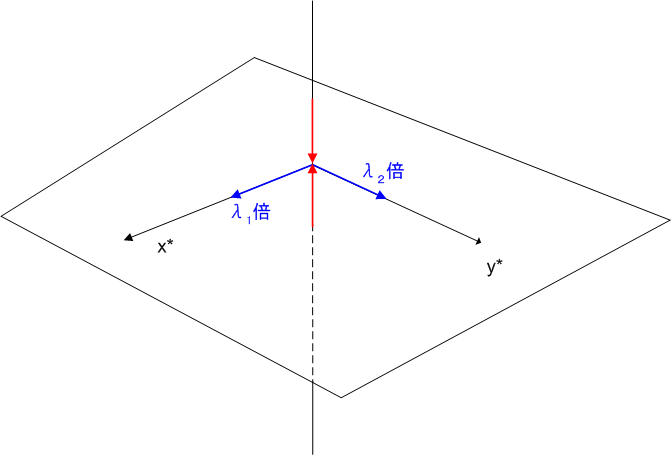
例えば,先ほどの図を一部再利用し,  方向の固有値が零である場合のテンソルの作用を図示してみたのが上図です.
方向の固有値が零である場合のテンソルの作用を図示してみたのが上図です.  方向の成分は全て零になってしまうので,どのようなベクトルも,
方向の成分は全て零になってしまうので,どのようなベクトルも, 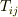 の作用を受けたら全て
の作用を受けたら全て 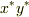 平面上の平面ベクトルになってしまいます.このように,固有方程式に零解が含まれる場合は,零解の個数分だけ,縮退が起こります.
平面上の平面ベクトルになってしまいます.このように,固有方程式に零解が含まれる場合は,零解の個数分だけ,縮退が起こります.