テンソル楕円体
この記事は, テンソルの主軸1 , テンソルの主軸2 の続きです.しばらく工学上の応用のため二階のテンソルばかりを扱い,行列の固有値や対角化など,行列の話題が出てきましたので,もう一度注意を喚起しておきます.
Important
テンソルを行列のことだと思ってはいけません
テンソルとは,あくまでも テンソルの概念 に紹介した定義を満たす量で,代数的には,多重線形性を満たすようにベクトル空間からテンソル積によって構成されるものでした.二階のテンソルを行列表記することが便利なため,どうしても応用的なテンソルの計算には行列がよく出て来ることになり,その結果『テンソルとは( 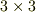 の)行列のことだ』と思い込んでいる人さえいるようなのです.恐ろしいことです.
の)行列のことだ』と思い込んでいる人さえいるようなのです.恐ろしいことです.
注意を喚起したところで,再び二階のテンソルの話に戻ります.これも工学上重要な応用的話題です^^
テンソル楕円体
対称テンソル 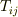 を使って表わされる次の二次曲面を考えます.
を使って表わされる次の二次曲面を考えます.

二階の対称テンソルですから, 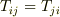 に注意すると,式
に注意すると,式 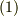 は一般に次のように展開できることが分かるでしょう. 二次曲線の係数 を参照して下さい
は一般に次のように展開できることが分かるでしょう. 二次曲線の係数 を参照して下さい
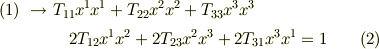
テンソル 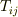 が固有値
が固有値 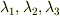 を持ち,主方向に座標系
を持ち,主方向に座標系 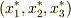 を取るとき,式
を取るとき,式 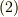 を次式のように簡単化することが出来るでしょう.
を次式のように簡単化することが出来るでしょう.
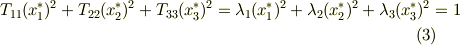
特に, 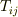 を対称テンソルだと仮定しているため,主軸は互いに直交しますので,
を対称テンソルだと仮定しているため,主軸は互いに直交しますので, 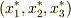 座標系として正規直交座標系を取ることが出来ます.これは大変に便利な話です.式
座標系として正規直交座標系を取ることが出来ます.これは大変に便利な話です.式 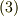 を次のように書き換えると,これが軸半径
を次のように書き換えると,これが軸半径 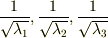 の楕円体を表わす式だということが分かると思います.
の楕円体を表わす式だということが分かると思います.
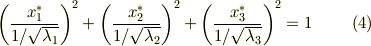
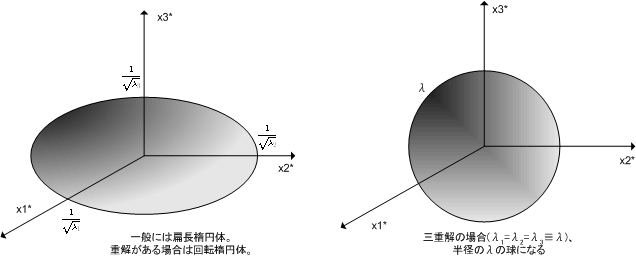
| [*] | テンソルの話題というより,単に行列の固有値と対角化の問題であるような気もします.冒頭の注意をもう一度思い出してください.応用上,応力テンソルや慣性モーメントを楕円体の形で表わすと便利な場合があります.例えば,自由に運動する剛体は,慣性楕円体が中心の高さを一定に保ちつつ,平面に滑らずに接して動くときの運動として幾何学的に捉えることが可能です.(楕円体の形は慣性モーメントによって,平面からの高さは剛体の持つ運動量によって決まります.楕円体を使って剛体の運動を考える方法を 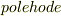 法と言います.)また,その他の楕円体の応用として,結晶の屈折率に異方性を示す屈折率楕円体というものもあります.これは,様々な方向から入射した直線偏光の屈折率をテンソル楕円体で表したもので,光が入射する方向からの楕円体の断面を見ることによって,幾何的に屈折率を知ることができます. 法と言います.)また,その他の楕円体の応用として,結晶の屈折率に異方性を示す屈折率楕円体というものもあります.これは,様々な方向から入射した直線偏光の屈折率をテンソル楕円体で表したもので,光が入射する方向からの楕円体の断面を見ることによって,幾何的に屈折率を知ることができます. |
補足:対称テンソルではない場合
最初にテンソル 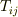 は対称テンソルだと仮定しましたが,これを一般のテンソルだとするとどうなるのでしょうか.この場合,
は対称テンソルだと仮定しましたが,これを一般のテンソルだとするとどうなるのでしょうか.この場合, 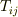 は対称部分
は対称部分 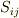 と反対称部分
と反対称部分 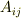 に分離可能です.( 対称テンソルと反対称テンソル 参照.)
に分離可能です.( 対称テンソルと反対称テンソル 参照.)

式 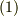 に式
に式 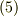 を代入してみます.
を代入してみます.
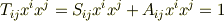
ここで, 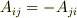 かつ
かつ 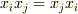 であることを考えると,
であることを考えると, 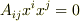 となってしまい,対称部分しか残らないことになります.すなわち,一般の二階のテンソルでも,互いに直交する主軸を持つテンソル楕円体を描くことは出来ますが,その楕円体の方程式はテンソルの対称部分のみによって規定されることになり,対称部分が共通なテンソルのテンソル楕円体は全て同一になります.
となってしまい,対称部分しか残らないことになります.すなわち,一般の二階のテンソルでも,互いに直交する主軸を持つテンソル楕円体を描くことは出来ますが,その楕円体の方程式はテンソルの対称部分のみによって規定されることになり,対称部分が共通なテンソルのテンソル楕円体は全て同一になります.