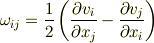対称テンソルと反対称テンソル
二階以上のテンソルで,成分の添字のうち,どれか二つを入れ替えても値が変わらないものを 対称テンソル と呼びます.

対称テンソルではどの添字を入れ替えても値が変わりません.一方,どれか添字を二つ入れ替えると符号が変わってしまうものを 反対称テンソル と呼びます.
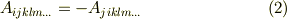
反対称テンソルでは添字を入れ替える回数が偶数回なら元と同じ符号,奇数回なら元と逆の符号になります.
例
いままでに何度も出てきているクロネッカーのデルタ 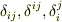 は対称テンソルです.計量テンソル
は対称テンソルです.計量テンソル 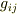 も,内積は可換ですから,定義より対称テンソルです.
も,内積は可換ですから,定義より対称テンソルです.
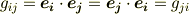
反対称テンソルの例はいままで出てきていませんが,二つのベクトル 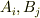 から次のような二階のテンソルを作ると反対称テンソルになります.添字を入れ替えて確認してみて下さい.
から次のような二階のテンソルを作ると反対称テンソルになります.添字を入れ替えて確認してみて下さい.
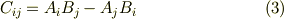
テンソルの対称性と座標変換
ある座標系で対称テンソルであるテンソルは,座標変換をしても対称テンソルのままです.このことは座標変換の式を眺めてみれば分かります.
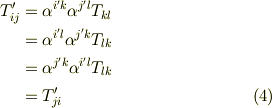
例として二階の対称テンソルを示しましたが,反対称テンソルも座標変換後によらず,常に反対称テンソルです.より高階のテンソルについても同様です.
theorem
座標変換しても,対称テンソルは対称テンソル,反対称テンソルは反対称テンソルのまま.
二階のテンソルの行列表示
二階のテンソルは行列で表示すると便利ですが,対称テンソル 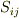 と反対称テンソル
と反対称テンソル 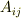 は行列表現で次のようになります.
は行列表現で次のようになります. 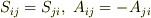 の関係を考えれば,なぜこうなるのかすぐに分かります.
の関係を考えれば,なぜこうなるのかすぐに分かります.
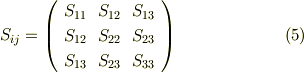
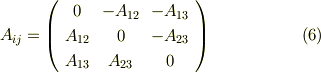
成分をよく見ると, 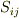 には
には 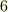 種類,
種類, 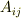 には
には 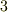 種類しかないことが分かるでしょう.なお,
種類しかないことが分かるでしょう.なお, 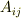 の成分では上三角の成分にマイナスをつけましたが,これは下三角の成分にマイナスをつけても構いません.この
の成分では上三角の成分にマイナスをつけましたが,これは下三角の成分にマイナスをつけても構いません.この 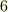 と
と 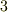 という数字を見て,何か思いませんか?一般の二階のテンソルは
という数字を見て,何か思いませんか?一般の二階のテンソルは 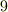 個の独立な成分を持ちましたから,一般の二階のテンソルを,
個の独立な成分を持ちましたから,一般の二階のテンソルを, 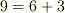 で,対称テンソルと反対称テンソルに分解できるのではないかという気がします.
で,対称テンソルと反対称テンソルに分解できるのではないかという気がします.
この予想は正しく,非常に単純なことに,一般に二階のテンソル 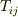 は常に対称テンソルと反対称テンソルの和に分解できます.
は常に対称テンソルと反対称テンソルの和に分解できます.

添字 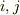 を入れ替えれば
を入れ替えれば 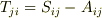 を得ますから,式
を得ますから,式 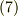 と連立して次式を得ます.
と連立して次式を得ます.
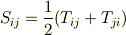
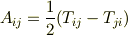
これは任意の二階のテンソル 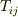 から,その対称部分と反対称部分を分離する公式だと言えます.
から,その対称部分と反対称部分を分離する公式だと言えます.
| [*] | 混合テンソルの場合,式 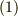 や や 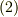 のように添字を入れ替えてみて良いのは,上下どちらか同じ側にある二つの添字に限ります.上下に分かれた添字を入れ替えてはいけません. のように添字を入れ替えてみて良いのは,上下どちらか同じ側にある二つの添字に限ります.上下に分かれた添字を入れ替えてはいけません. |
| [†] | 連続体力学において,連続体の変形を表わすのに二階のテンソルが活躍します.連続体の変位を 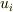 ,座標成分を ,座標成分を 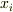 ,歪み速度を ,歪み速度を 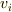 と置き,以下のようなテンソルが使用されます.テンソルの知識が何も無いと,変な定義だと思うでしょうが,変位を表わすテンソル と置き,以下のようなテンソルが使用されます.テンソルの知識が何も無いと,変な定義だと思うでしょうが,変位を表わすテンソル 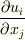 と変位の速度を表わすテンソル と変位の速度を表わすテンソル 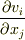 をそれぞれ対称部分と反対称部分に分離したものが,歪みテンソル,渦度テンソル,歪み速度テンソル,歪み勾配テンソルと呼ばれる諸量です.連続体の場合,縦の力が横の変位を起こしたり,その逆があったりと,真っ直ぐ押して真っ直ぐ凹む以外の変形が起きます.このような現象を表現するには二階のテンソルが適しているわけですが,対称テンソルと反対称テンソルに分離することで,変形による変位と,連続体全体が回転したことによる変位とを分離して扱うことが出来るようになります.テンソルを対称部分と反対称部分に分離する例として連続体力学を挙げましたが,詳しくは連続体力学,材料力学などの教科書を参照してください.また,反対称テンソルのベクトルへの作用が微小回転に等しいことは, 無限小回転 を参照してしてください. をそれぞれ対称部分と反対称部分に分離したものが,歪みテンソル,渦度テンソル,歪み速度テンソル,歪み勾配テンソルと呼ばれる諸量です.連続体の場合,縦の力が横の変位を起こしたり,その逆があったりと,真っ直ぐ押して真っ直ぐ凹む以外の変形が起きます.このような現象を表現するには二階のテンソルが適しているわけですが,対称テンソルと反対称テンソルに分離することで,変形による変位と,連続体全体が回転したことによる変位とを分離して扱うことが出来るようになります.テンソルを対称部分と反対称部分に分離する例として連続体力学を挙げましたが,詳しくは連続体力学,材料力学などの教科書を参照してください.また,反対称テンソルのベクトルへの作用が微小回転に等しいことは, 無限小回転 を参照してしてください. |
【歪みテンソル】
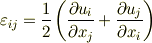
【渦度テンソル】
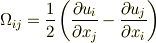
【歪み速度テンソル】
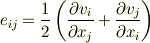
【速度勾配テンソル】