流れ関数
ベクトル場とそのポテンシャル関数に関する一つの応用として,流体力学における二次元平面流を考えます.このベクトル場 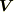 は管状であるとします.(
は管状であるとします.( 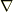 も二次元であることに注意して下さい.)
も二次元であることに注意して下さい.)
非圧縮流の連続の式
いま,流れ場 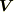 の中に適当な流管を取ります.質量保存則より『流管のどの断面を取っても,単位時間に断面を過ぎる質量は等しい』と考えることが出来ます.これを式にすると次のようになります.流体の密度を
の中に適当な流管を取ります.質量保存則より『流管のどの断面を取っても,単位時間に断面を過ぎる質量は等しい』と考えることが出来ます.これを式にすると次のようになります.流体の密度を 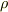 とします.
とします.

流管の考え方については ベクトル場の流線と流管 を参照して下さい.式 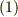 は,流れ場が連続であれば必ず成り立つことが要請されるもので, 連続の式 と呼ばれます.要するに質量保存則なわけですが,流体力学の大事な基礎方程式の一つです.特に,非圧縮流の場合,
は,流れ場が連続であれば必ず成り立つことが要請されるもので, 連続の式 と呼ばれます.要するに質量保存則なわけですが,流体力学の大事な基礎方程式の一つです.特に,非圧縮流の場合,  ですので,
ですので, 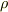 を外に出して次のように簡単化できます.
を外に出して次のように簡単化できます.

これは 非圧縮流の連続の式 ですが,同時に 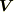 が管状であることも示しています.質量保存の法則はどんな流体にも成り立ちますから,流体力学の立場では,管状ベクトル場とは非圧縮流の流れを意味すると考えても良さそうです.
が管状であることも示しています.質量保存の法則はどんな流体にも成り立ちますから,流体力学の立場では,管状ベクトル場とは非圧縮流の流れを意味すると考えても良さそうです.
二次元流と流れ関数
前セクションの内容は三次元の流れでも成り立つものでしたが,ここでは特に二次元平面流を考えます. 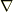 も二次元になることに注意して下さい.
も二次元になることに注意して下さい.
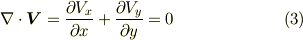
このとき, 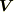 の成分を,スカラーポテンシャル
の成分を,スカラーポテンシャル 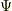 を用いて次のように表わすことができます.
を用いて次のように表わすことができます.
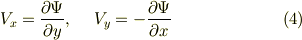
この 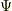 を 流れ関数 と呼びます.式
を 流れ関数 と呼びます.式 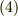 が自動的に式
が自動的に式 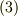 を満たすことを確認してみて下さい.流れ関数は,次のようにベクトルポテンシャルの形で与えることもできます.この方が,すっきりと覚えやすいかも知れません.(管状ベクトル場にベクトルポテンシャルが存在することについては, 管状ベクトル場 を参照して下さい.)
を満たすことを確認してみて下さい.流れ関数は,次のようにベクトルポテンシャルの形で与えることもできます.この方が,すっきりと覚えやすいかも知れません.(管状ベクトル場にベクトルポテンシャルが存在することについては, 管状ベクトル場 を参照して下さい.)
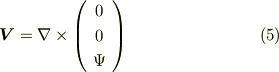
もしくは,次のように表現することも可能です.
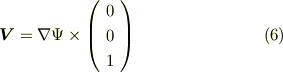
流線と流れ関数の関係
ついでに,流れ関数の物理的意味も考えておきます.  の中に置かれた曲線
の中に置かれた曲線  を単位時間当たりに通過する全流量
を単位時間当たりに通過する全流量  を求めてみます.
を求めてみます.  は二次元平面流なので,
は二次元平面流なので,
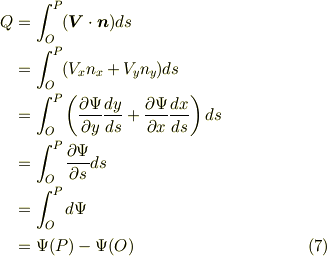
これより次のことが言えます.
theorem
二次元非圧縮流の流れの中に二点 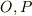 を取るとき,
を取るとき, 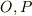 を結ぶ任意の曲線を単位時間当たりに通過する流量は流れ関数の差
を結ぶ任意の曲線を単位時間当たりに通過する流量は流れ関数の差  で表わされ,曲線の形にはよらない.
で表わされ,曲線の形にはよらない.
また,同一の流線上では流量が零なので,  が言えます.これも重要な性質です.流れ関数の物理的意味が,少し明らかになって来たでしょうか.
が言えます.これも重要な性質です.流れ関数の物理的意味が,少し明らかになって来たでしょうか.
theorem
同一の流線の上では,  が成り立ちます.逆に
が成り立ちます.逆に  は,一本の流線を表わします.
は,一本の流線を表わします.
ベクトル場をポテンシャル関数で表現する一例として,二次元非圧縮流の流れ関数を取り上げてみました.より詳しくは,きちんと流体力学の教科書を参考にして下さい.
ノイマン問題
流れ関数は,どのような境界条件を満たすのでしょうか?物理的状況を考えてみると,水の流れは,境界(つまり,水槽の壁や川底などの固体壁)を突き抜けて流れることはできません.境界では,必ず境界に沿った方向(接線方向)に流れ,境界の法線方向の速度成分は持たない,ということです.これを式で書くと次のように表わせます.

ここで,もし流れ場が 層状ベクトル場 だとすると, 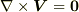 が要請されます.流れ関数の表わす流れが二次元平面流であることに注意すると,この層状の条件は次のようになります.
が要請されます.流れ関数の表わす流れが二次元平面流であることに注意すると,この層状の条件は次のようになります.

式 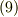 の
の  成分だけ考えて,次式に帰着します.ただし,
成分だけ考えて,次式に帰着します.ただし,  は二次元ラプラシアンの意味だとします.
は二次元ラプラシアンの意味だとします.
式  より,二次元層状ベクトル場の流れ関数は,ノイマン問題の解として与えられるということが分かりました.(ノイマン問題の定義は ラプラス場 の最後に紹介しています.)このようにして,流れ場を求める問題が,微分方程式を境界条件の下に解くという問題に帰着してしまったわけです.流れの様子を生き生きと想像していた人にとって,もしかして微分方程式を解くという作業は,とても静的で無機質に思えるかも知れません.しかし,このようにして流れを微分方程式に帰着できるというのが,ポテンシャルを導入した旨味なのです.ポテンシャル論をもっと勉強していくと,ラプラス方程式に代表される様々な微分方程式を,様々な境界条件下で解くといった問題が主なトピックになってきます.
より,二次元層状ベクトル場の流れ関数は,ノイマン問題の解として与えられるということが分かりました.(ノイマン問題の定義は ラプラス場 の最後に紹介しています.)このようにして,流れ場を求める問題が,微分方程式を境界条件の下に解くという問題に帰着してしまったわけです.流れの様子を生き生きと想像していた人にとって,もしかして微分方程式を解くという作業は,とても静的で無機質に思えるかも知れません.しかし,このようにして流れを微分方程式に帰着できるというのが,ポテンシャルを導入した旨味なのです.ポテンシャル論をもっと勉強していくと,ラプラス方程式に代表される様々な微分方程式を,様々な境界条件下で解くといった問題が主なトピックになってきます.