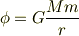スカラーポテンシャル
スカラー場 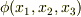 を考えます.
を考えます. 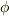 はつまり,
はつまり, 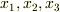 を変数とする関数で,
を変数とする関数で, 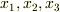 を座標変数だとすれば,空間の各点に対して値を一つ返す関数だということになります.この
を座標変数だとすれば,空間の各点に対して値を一つ返す関数だということになります.この 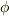 に
に 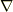 を作用させると,次のようにベクトルが得られます.
を作用させると,次のようにベクトルが得られます.
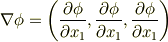
ベクトル 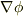 は,一般的には空間の各点で向きや大きさを変えるベクトルですから, ベクトル場 になります.(偏微分をいちいち分数の形で書くのは面倒なので,
は,一般的には空間の各点で向きや大きさを変えるベクトルですから, ベクトル場 になります.(偏微分をいちいち分数の形で書くのは面倒なので, 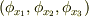 のように,右下に小さく変数を書いて略記することもあります.)
のように,右下に小さく変数を書いて略記することもあります.)
| [*] | もちろん,  が一意的に微分可能な関数であることが前提になっています. が一意的に微分可能な関数であることが前提になっています.  が『ほとんど微分可能なのだけど,一点だけでは微分不能である』といった関数である場合,その点だけではベクトル場が定義できません.そんな点を特異点と呼びます.幾つかそんな点が混ざっているくらいなら,通常,議論にはあまり困りません.ひとまず が『ほとんど微分可能なのだけど,一点だけでは微分不能である』といった関数である場合,その点だけではベクトル場が定義できません.そんな点を特異点と呼びます.幾つかそんな点が混ざっているくらいなら,通常,議論にはあまり困りません.ひとまず 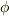 の関数としての性質についてうるさいことは言わず,常識的に『素直な関数』だとして,以下の議論を進めます. の関数としての性質についてうるさいことは言わず,常識的に『素直な関数』だとして,以下の議論を進めます. |
スカラーポテンシャル
逆に,ベクトル場  が与えられたとき,これを
が与えられたとき,これを 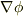 の形で表わせれば便利そうです.次式のようにベクトル場を
の形で表わせれば便利そうです.次式のようにベクトル場を 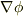 の形で表わす
の形で表わす 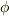 のことを,このベクトル場の スカラーポテンシャル と呼びます.スカラーと付くのは,
のことを,このベクトル場の スカラーポテンシャル と呼びます.スカラーと付くのは, 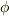 がスカラー関数だからです.
がスカラー関数だからです.
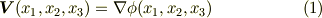
もっとも,物理学では右辺に  をつけて使う方が多いかも知れません.数学的には,符号の正負は本質的ではないですが,物理学の慣習では,恐らく以下のようなイメージに基づいた計算の便宜のため,たいてい
をつけて使う方が多いかも知れません.数学的には,符号の正負は本質的ではないですが,物理学の慣習では,恐らく以下のようなイメージに基づいた計算の便宜のため,たいてい  をつけます.一般に,物理に出て来るベクトル場は,何か『流れ』を表わすと考えて良いと思います.(電流など,目に見えない流れも含みます.)
をつけます.一般に,物理に出て来るベクトル場は,何か『流れ』を表わすと考えて良いと思います.(電流など,目に見えない流れも含みます.)

流れは,ポテンシャルが高い方から低い方へ流れると考えたい.
目に見えないような流れも含め,水流からの連想なのか,『流れは,ポテンシャルの高い方から低い方へ流れる』と考えることが自然であり,普通です.この,高い方から低い方,という向きは,ポテンシャルの値が減っていく向きですから, 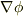 と逆方向になります.このような物理的イメージのため,スカラーポテンシャルの定義式には
と逆方向になります.このような物理的イメージのため,スカラーポテンシャルの定義式には  がついているとのです.
がついているとのです.
ベクトル場 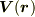 が与えられたとき,一般に
が与えられたとき,一般に 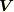 がスカラーポテンシャルを持つとは限りません.スカラーポテンシャルが無い場合や,一意的に決まらない場合もあります.(ベクトル場からスカラーポテンシャルを求める操作は,最後のセクションで示すように偏微分方程式を解く作業になります.この偏微分方程式が解を持たない場合や,解が一意的に求まらない場合はスカラーポテンシャルが決まりません.)スカラーポテンシャルを持つベクトル場を特に 保存ベクトル場 と呼びます.
がスカラーポテンシャルを持つとは限りません.スカラーポテンシャルが無い場合や,一意的に決まらない場合もあります.(ベクトル場からスカラーポテンシャルを求める操作は,最後のセクションで示すように偏微分方程式を解く作業になります.この偏微分方程式が解を持たない場合や,解が一意的に求まらない場合はスカラーポテンシャルが決まりません.)スカラーポテンシャルを持つベクトル場を特に 保存ベクトル場 と呼びます.
| [†] | 数学系の本にはスカラーポテンシャルの符号が  のものも多いです.符号の問題は本質的ではありませんが,混乱すると面倒です.自分で色々な本を読むときには注意して下さい. のものも多いです.符号の問題は本質的ではありませんが,混乱すると面倒です.自分で色々な本を読むときには注意して下さい. |
スカラーポテンシャルの求め方
スカラーポテンシャルを実際に求める方法を考えてみましょう.ベクトル場 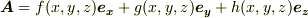 があったとします.このとき定義より,もしこのベクトル場にスカラーポテンシャル
があったとします.このとき定義より,もしこのベクトル場にスカラーポテンシャル 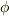 が存在するならば,次式がなりたつはずです.
が存在するならば,次式がなりたつはずです.



ここで, 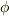 を滑らかな関数だとすれば
を滑らかな関数だとすれば  がなりたつので,式
がなりたつので,式 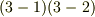 について次の関係がなりたつことが要請されます.
について次の関係がなりたつことが要請されます.

同様に,次の二式も必要です.


これらが全て成り立っていなければ保存ベクトル場にはなりません.結構,きつい条件ですね.
| [‡] | ポテンシャル関数は滑らかだと勝手に仮定しましたが,ポテンシャル関数は微分可能でなければ意味がありませんから,これは妥当な仮定だと思います.偏微分の順番を変更できるのは,関数が滑らかな場合です. |
練習問題
- ベクトル場
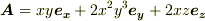 はスカラーポテンシャルを持たないことを示して下さい.
はスカラーポテンシャルを持たないことを示して下さい. - ベクトル場
 のスカラーポテンシャルを求めてください.
のスカラーポテンシャルを求めてください.
保存ベクトル場を積分してみる
保存ベクトル場を,点 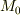 から点
から点 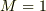 まで積分してみると,面白いことが分かります.
まで積分してみると,面白いことが分かります.
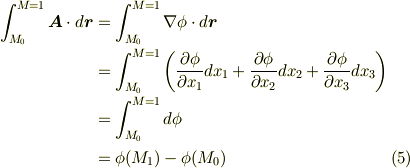
最終的にこの積分の値は積分経路によらず,積分の始点と終点の値だけで決まることになります.二行目から三行目で,全微分の関係  を使ったことに注意して下さい.ベクトル場の問題にスカラー・ポテンシャルを持ち込むことで享受できる利点の一つに,ベクトルの積分に際して実質的に積分計算をする手間をはぶき, ポテンシャルの差だけで議論できる ということがあります.
を使ったことに注意して下さい.ベクトル場の問題にスカラー・ポテンシャルを持ち込むことで享受できる利点の一つに,ベクトルの積分に際して実質的に積分計算をする手間をはぶき, ポテンシャルの差だけで議論できる ということがあります.
| [§] | 先ほど考えた重力の例を思い出してください.質点の位置エネルギー(重力のポテンシャル)は高さだけで決まり,持ち上げる経路にはよらないということを高校の物理でも習いますが,これは,重力ポテンシャルがスカラー・ポテンシャルだからこんな楽な考え方が出来るのです.また,ポテンシャルの定義として 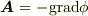 のようにマイナスの符号をつけると,ポテンシャルの和を『足し算』の形で表現でき,『流れは高い方から低い方へ流れる』というイメージに従えば,ポテンシャルの高さを足すというイメージで考えることが出来るようになります. のようにマイナスの符号をつけると,ポテンシャルの和を『足し算』の形で表現でき,『流れは高い方から低い方へ流れる』というイメージに従えば,ポテンシャルの高さを足すというイメージで考えることが出来るようになります. |
| [¶] | 全微分が積分経路によらない,というのは次のように考えることも出来ます.関数 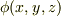 を,座標変換して を,座標変換して 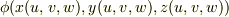 と表わせるとします.このとき,全微分を と表わせるとします.このとき,全微分を  と表わしても, と表わしても, 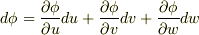 と表わしても同じことです.一方は と表わしても同じことです.一方は 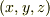 座標系で,もう一方は 座標系で,もう一方は 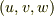 座標系で表わされているのですから,これは『全微分は座標変換に対して不変である』ということになります.(ただし,この座標変換は連続で滑らかな一対一の変換だとします.)実は,全微分は一次微分形式という別名も持っています.微分形式の理論は,座標変換によらない形で微分方程式を定式化するための強力な道具で,全微分はその形式になっているのですね. 座標系で表わされているのですから,これは『全微分は座標変換に対して不変である』ということになります.(ただし,この座標変換は連続で滑らかな一対一の変換だとします.)実は,全微分は一次微分形式という別名も持っています.微分形式の理論は,座標変換によらない形で微分方程式を定式化するための強力な道具で,全微分はその形式になっているのですね. |
もし,閉曲線にそってベクトルを周回積分するなら,始点と終点が同じですから積分は零になります.これも便利な結果です.
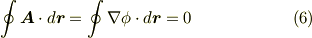
少し先走ってベクトルの積分を考えてしまいましたが,式 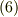 の形の積分は ベクトルの線積分と周回積分 できちんと勉強します.
の形の積分は ベクトルの線積分と周回積分 できちんと勉強します.
| [#] | さらに発展的な話になりますが,ベクトル場 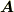 が定義されている領域が単連結(位相的に中身の詰まった領域)ならば式 が定義されている領域が単連結(位相的に中身の詰まった領域)ならば式 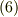 が成り立ちますが, 単連結 ではない領域で が成り立ちますが, 単連結 ではない領域で 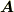 が定義されているような場合,必ずしも式 が定義されているような場合,必ずしも式 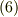 の結果は使えません.ちょっと難しい話に感じるかも知れませんが,積分領域の幾何学的性質についても,いずれもう少しきちんと勉強します. の結果は使えません.ちょっと難しい話に感じるかも知れませんが,積分領域の幾何学的性質についても,いずれもう少しきちんと勉強します. |

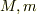 の二つの質点を考え,中心間の距離を
の二つの質点を考え,中心間の距離を  とします.質点
とします.質点 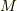 にベクトルの原点を置き,
にベクトルの原点を置き, 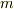 へ向かう単位ベクトルを
へ向かう単位ベクトルを 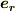 とするとき,質点
とするとき,質点 
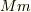 間の距離
間の距離  の大きさは変わりますので,
の大きさは変わりますので, 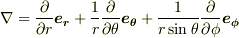 (詳しくは
(詳しくは 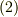 は次のように書き換えられます.
は次のように書き換えられます.
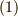 と見比べて,重力のポテンシャルは次式であると分かります.この形を,すでに力学で勉強したことのある人も多いでしょう.
と見比べて,重力のポテンシャルは次式であると分かります.この形を,すでに力学で勉強したことのある人も多いでしょう.