スカラー場と勾配
スカラー場 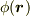 を考えます.
を考えます.
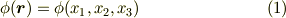
スカラー場とは,空間の各点 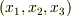 でスカラーが一つ決まるような関数を言います.ある点では
でスカラーが一つ決まるような関数を言います.ある点では 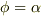 ,別の点では
,別の点では 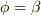 という具合です.しかし
という具合です.しかし 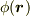 の取る値を全部調べてグラフにすると
の取る値を全部調べてグラフにすると 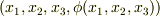 という四次元のグラフになってしまい,絵に描けないので,何だか何だかよく分かりません.
という四次元のグラフになってしまい,絵に描けないので,何だか何だかよく分かりません.
そこで,代わりにあるスカラー値,例えば 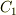 を考え,
を考え, 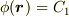 を満たす
を満たす 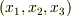 を全てグラフに描いてみることにします.これは何らかの三次元曲面を表わす式となり,グラフも目で見て分かります.その代わり,全体の様子を知ろうと思えば,様々なスカラー値に対して,たくさん曲面を描かなければなりません.
を全てグラフに描いてみることにします.これは何らかの三次元曲面を表わす式となり,グラフも目で見て分かります.その代わり,全体の様子を知ろうと思えば,様々なスカラー値に対して,たくさん曲面を描かなければなりません.
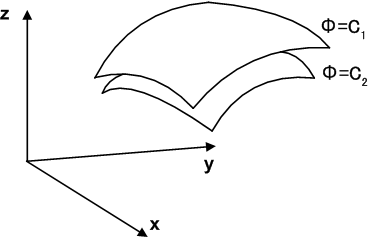
これらの面を スカラー場の等位面 と呼びます.(物理学の文脈では,スカラー場はしばしばポテンシャルと呼ばれ,このような面は 等ポテンシャル面 と呼ばれます.)上図は等位面の様子を示してみたものです. 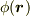 が連続関数ならば,
が連続関数ならば, 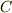 の値を少しずつずらしてやって,様々な等位面をタマネギの皮が重なるような感じに書けます.詳しい地図には等高線という線が引いてありますが,等位面とは,等高線の三次元版だと思えば良いでしょう.
の値を少しずつずらしてやって,様々な等位面をタマネギの皮が重なるような感じに書けます.詳しい地図には等高線という線が引いてありますが,等位面とは,等高線の三次元版だと思えば良いでしょう. 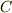 を一定間隔で変化させて様々な等位面を重ねて描く時, 等位面の密度が濃い(隣の等位面との距離が近い)部分は
を一定間隔で変化させて様々な等位面を重ねて描く時, 等位面の密度が濃い(隣の等位面との距離が近い)部分は 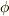 の変化が激しく,逆に等位面の密度が薄い(隣の等位面との距離が遠い)部分は
の変化が激しく,逆に等位面の密度が薄い(隣の等位面との距離が遠い)部分は 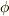 の変化が緩やかな部分だと考えることができます.これは,等高線の密度が濃い部分は山の勾配がきつく,密度が薄い部分の勾配が緩いのと同じ理屈ですね.
の変化が緩やかな部分だと考えることができます.これは,等高線の密度が濃い部分は山の勾配がきつく,密度が薄い部分の勾配が緩いのと同じ理屈ですね.
| [*] | ただし,地図で『勾配が急だ』『勾配が緩い』などというのは,"高さの勾配"の話をしています.これは,『高さ』が位置の関数になっていると考えられます.一般に式 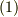 のように書いた関数 のように書いた関数 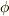 は,高さに限らず,重力,電場,磁場など色々な場を表わす場合があります.電場や磁場など目に見えない世界になると急にイメージが湧かなくなる人がいますが,基本は上の図と,地図の等高線のイメージです. は,高さに限らず,重力,電場,磁場など色々な場を表わす場合があります.電場や磁場など目に見えない世界になると急にイメージが湧かなくなる人がいますが,基本は上の図と,地図の等高線のイメージです. |
| [†] | 新田次郎氏の小説『孤高の人』に,主人公・加藤文太郎が,会社の先輩に『地図遊び』という遊びを教わるシーンがあります.地図の等高線をじっくりながめ,地形の起伏が目に浮かび,山が川がどこをどう流れているか,光が当たると影がどう伸びるかという立体的な様子を,山登りに行く前にイメージするという遊びなんですが,かなり高度な立体図形の把握能力が求められそうです.読者のみなさんも,等位面を使って『地図遊び』をしてみて下さい.電場や磁場をいきいきと想像できる人になりたいものです. |
等位面が交差することはありません.というのは,最初に『 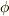 に対し空間の各点
に対し空間の各点 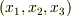 でスカラーが 一つ決まる 』と仮定しているからです.
でスカラーが 一つ決まる 』と仮定しているからです.
スカラー場の勾配
私達は,スカラー場 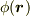 の値に応じて決まる曲面(等位面)を考え,等位面の粗密によってスカラー場の変化の具合を考えました.面の粗密に応じて変化の具合が分かるというのは,ちょうど地図の等高線と同じアイデアでした.そこで,次の興味が湧いてくるのは,実際に関数
の値に応じて決まる曲面(等位面)を考え,等位面の粗密によってスカラー場の変化の具合を考えました.面の粗密に応じて変化の具合が分かるというのは,ちょうど地図の等高線と同じアイデアでした.そこで,次の興味が湧いてくるのは,実際に関数 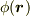 の変化具合を計算してみることです.
の変化具合を計算してみることです.
もしも 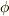 が一変数の関数,例えば
が一変数の関数,例えば 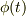 ならば,任意の点(例えば
ならば,任意の点(例えば 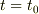 )における勾配は,
)における勾配は, 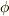 の微係数を計算して
の微係数を計算して 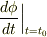 として調べられるでしょう.いま,私達が考えなければならないのは,
として調べられるでしょう.いま,私達が考えなければならないのは, 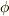 が
が 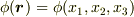 という三変数の関数であることです.とりあえず,三種類の偏導関数を考えてみましょう.
という三変数の関数であることです.とりあえず,三種類の偏導関数を考えてみましょう.
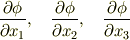
これら三種類の偏導関数の組は 共変ベクトルと反変ベクトル の記事の最後の例で示したように,ベクトルになります.
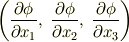
このベクトルを 勾配ベクトル と呼び,次のように  を用いて表わします.(英語で勾配のことを
を用いて表わします.(英語で勾配のことを 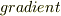 と言います.)
と言います.)
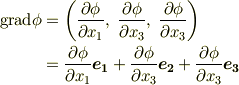
もしくは,微分演算子を組み合わせたベクトルを 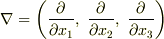 と置き,次のように書いても同じことです.この記号
と置き,次のように書いても同じことです.この記号 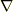 を ナブラ もしくは ハミルトンの演算子 と呼びます.(ナブラを,
を ナブラ もしくは ハミルトンの演算子 と呼びます.(ナブラを, 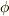 のようなスカラーに作用させる時
のようなスカラーに作用させる時  と書くのです.ベクトルに作用させるときは
と書くのです.ベクトルに作用させるときは 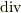 と書きます.
と書きます. 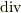 はまた後で勉強します.一長一短あるのですが,今後,
はまた後で勉強します.一長一短あるのですが,今後,  と書くより,記号
と書くより,記号 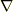 を使う方が多いと思います.)
を使う方が多いと思います.)
| [‡] | ナブラはベクトルですから,ベクトルの性質を持ち,ベクトルで成り立った定理を使うことができます.そういう意味で,ナブラだって疑いなく一種のベクトルです.ただし,ナブラの演算で注意しなければならないのは,ナブラの右側から何かを掛けると,微分されてしまうという性質です.ナブラに左から何か掛けてもそれは単なる積です.こうした『微分演算子』という役割を持つため,ナブラを掛け算するときには注意が必要です.たとえば内積も可換ではなくなります.順々に 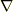 を使った計算を見ていくので馴れていくとは思いますが,このことを念頭に置いておいて下さい. よくある間違い を参考にしてください. を使った計算を見ていくので馴れていくとは思いますが,このことを念頭に置いておいて下さい. よくある間違い を参考にしてください. |