二次曲線の係数
私達は,座標系を直交変換する際の変換則を使ってテンソルの概念を定義しました.例えば二階のテンソルとは,添字 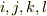 を使えば,変換係数
を使えば,変換係数 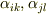 を使って次式に従って座標変換される量(ここでは
を使って次式に従って座標変換される量(ここでは 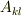 )のことでした.
)のことでした.
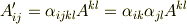
ピンと来ない人は,もう一度 テンソルの概念 を復習してください.この変換則自体は,添字にだけ注意していればそんなに難しいものではありません.形式的には,右辺で上下に分かれている添字を消すと左辺になります.しかし,実際にこの変換則に従う量にはどのような例があるのでしょうか?見るからに添字が付いていれば『いかにも!?』という臭いがしますが,添字がついていないとテンソルだなんて気づかないかも知れません.既に高校で習ったような量にも,実は二階のテンソルがある,という例をこの記事では取り上げます.
楕円の方程式
原点を中心とし,  軸と
軸と 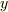 軸の方向に,長軸と短軸を向けた楕円の方程式は一般に次のように表わせます.
軸の方向に,長軸と短軸を向けた楕円の方程式は一般に次のように表わせます.

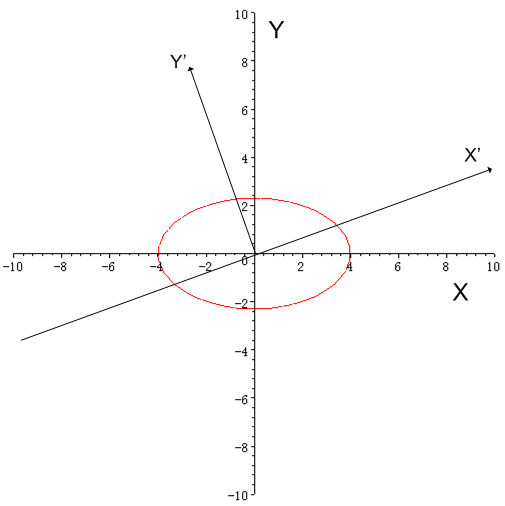
この同じ楕円を, 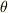 度だけ傾いた
度だけ傾いた 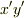 座標系から記述すると,式
座標系から記述すると,式 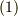 に
に 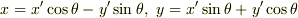 を代入して次式のようになるでしょう.
を代入して次式のようになるでしょう.
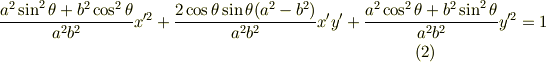
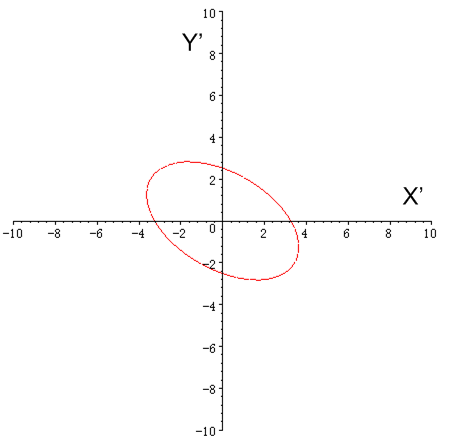
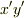 座標系からはこう見える.
座標系からはこう見える.
式  は式
は式 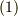 に比べて大変複雑に見えますが,同じ楕円を記述しているわけですから,式
に比べて大変複雑に見えますが,同じ楕円を記述しているわけですから,式 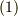 の係数と式
の係数と式  の係数は無関係ではないはずです.その変換関係を考えてみましょう.
の係数は無関係ではないはずです.その変換関係を考えてみましょう.  を
を 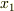 ,
, 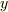 を
を 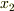 と名前をつけ直し,式
と名前をつけ直し,式 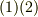 をそれぞれ次のように表現してみます.
をそれぞれ次のように表現してみます.
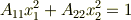

ただし,係数 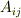 の添字は『
の添字は『 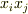 の項にかかる係数』という意味です.縮約を使えば,さらに簡単に表現できるでしょう.これを式
の項にかかる係数』という意味です.縮約を使えば,さらに簡単に表現できるでしょう.これを式 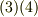 とします.また,いま図のように直交座標系を考えていますので,添字の上下による区別は考えず,全て右下に書くことにします.(例えば 双対基底の図形的関係 を参照して下さい.)
とします.また,いま図のように直交座標系を考えていますので,添字の上下による区別は考えず,全て右下に書くことにします.(例えば 双対基底の図形的関係 を参照して下さい.)


なんだかテンソルの臭いがぷんぷんして来ましたね.座標系の直交変換は,適当な二階のテンソル 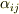 を使って
を使って 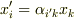 のように表現できるはずですから,これを式
のように表現できるはずですから,これを式 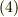 に代入してみます.
に代入してみます.
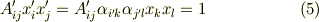
中辺はダッシュのついていない座標系  で表されています.そこで式
で表されています.そこで式 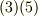 の係数を比較して次式を得ます.
の係数を比較して次式を得ます.
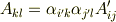
これは二階のテンソルの定義式になっていますから,楕円の方程式の係数 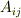 は 二階のテンソルだ ということが分かりました.図形の方程式の係数はただの数字だと思っていた人がいると思いますが,実はテンソルなのでした.テンソルの定義でもある,座標変換の式に少し慣れてきましたか?
は 二階のテンソルだ ということが分かりました.図形の方程式の係数はただの数字だと思っていた人がいると思いますが,実はテンソルなのでした.テンソルの定義でもある,座標変換の式に少し慣れてきましたか?
| [*] | この結果の意味するところは,『楕円の方程式の係数も座標変換に際してある変換則に従って変化する』ということです.(そして,その変換則はテンソルの変換則として表現できるということです.)座標変換をしたところで,同じ図形を表現する方程式には変わりないわけですから,係数が図形の形や性質を崩さないように一定の変換法則に従うのはむしろ当然のことだと言えるでしょう.二次曲線は一般に  の形で表現できますが,例えば の形で表現できますが,例えば 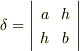 という量は座標系の平行移動や回転変換(つまり直交変換)に対して不変です.( テンソル不変量 を参照下さい.)計算は少々面倒ですが,式 という量は座標系の平行移動や回転変換(つまり直交変換)に対して不変です.( テンソル不変量 を参照下さい.)計算は少々面倒ですが,式  と と  で で 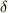 が一定であることを確認してみて下さい. が一定であることを確認してみて下さい. |
| [†] | 例として楕円だけ取り上げましたが,双曲線や放物線の方程式でも同様の議論ができますので,自分で考えてみてください.また,式 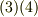 の表式で の表式で 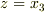 を付け加えれば,楕円体面や双曲面といった二次曲面を表わす方程式に対しても同じ結果が導けます. を付け加えれば,楕円体面や双曲面といった二次曲面を表わす方程式に対しても同じ結果が導けます. |