ポテンシャルと流線

この記事は，一つ前の 多価関数のポテンシャル の内容の続きになっています．

一価ポテンシャルの流線

単連結な領域で定義されたポテンシャル場 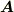\bm{A} は一価関数によって与えることができました．そして，このポテンシャル場には次のような大きな特徴がありました．

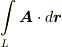  1. 線積分 \int \limits_{L} \bm{A} \cdot d\bm{r} は積分経路によらない．
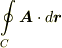  2. 周回積分 \ointop \limits_{C} \bm{A} \cdot d\bm{r} は，積分経路によらず常に 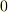0 になる．

本当はこの二つは同じことを言っているんですが（１の線積分で始点＝終点としたら，２の周回積分になりますからね），非常に大事な性質なので別に書いてみました．この二番目の性質より，次のことが言えます．

theorem

単連結な領域で，一価ポテンシャル関数によって与えられる流れ場に，閉じた流線はありません．

proof

もし閉曲線となる流線があれば，その流線に沿って線積分を考えるとき，流れと同じ方向なら 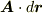\bm{A}\cdot d\bm{r} は常に正，流れと逆方向なら常に負となり，どっち向きに一周しても 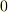0 にはなりません．よって，流線は閉曲線にはなりません．■

例えば， 多価関数のポテンシャル の最後で取り上げた，直線電流がビオ＝サヴァールの法則によって作る磁場は，電流を中心とする同心円状の閉曲線になりますから，この流れを一価ポテンシャル関数で表わすのは無理で，多価ポテンシャル関数による表現になるわけです．

theorem

流線が閉じる流れをポテンシャルで表わせるとすれば，それは多価関数になります．

[*]ただし，多重連結領域の多価ポテンシャル関数も，工夫して（例えば穴を塞ぐなどして）領域を単連結に直すことで一価関数にすることが出来ます．そうすると，同時に閉曲線状の流線は有限領域には描けなくなります．こういった操作については，難しいのでここでは取り上げません．詳しくは，また機会があれば電磁気学の分野などで，具体的な問題とともに考えてみたいと思います．