スカラーポテンシャル場と層状ベクトル場

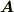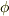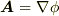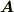ベクトル場 $\bm{A}$ が，スカラーポテンシャル $\phi$ によって $\bm{A} = \nabla \phi$ と表わせるとき， $\bm{A}$ を スカラーポテンシャル場 と呼びました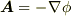．（ $\bm{A} = - \nabla \phi$ と定義しても構いません．物理学での応用上はをつけることの方が多いと思いますが，符号は数学的には本質的ではありません．ここでは，マイナスはつけないで議論します．）スカラーポテンシャルを定義すると，たった一つのスカラー関数からベクトル場の成分が求められるという便利さがありました．

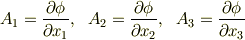
$A_{1}= \frac{\partial \phi}{\partial x_{1}}, \ \ A_{2}= \frac{\partial \phi}{\partial x_{2}}, \ \ A_{3}= \frac{\partial \phi}{\partial x_{3}}$

また，スカラーポテンシャル場に著しい特徴として， 線積分が経路によらない というものがありました．さらに，スカラーポテンシャル場の周回積分は常に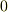になるのでした．（詳しくはスカラーポテンシャルを参照して下さい．）

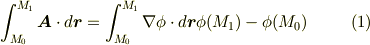
$\int_{M_{0}}^{M_{1}} \bm{A}\cdot d\bm{r}=\int_{M_{0}}^{M_{1}} \nabla \phi \cdot d\bm{r} \phi (M_{1}) - \phi (M_{0}) \tag{1}$

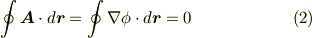
$\ointop \bm{A}\cdot d\bm{r} &= \ointop \nabla \phi \cdot d\bm{r} = 0 \tag{2}$

ここまでは復習事項です．一般に，至るところ 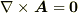$\nabla \times \bm{A}=\bm{0}$ であるベクトル場を， 層状ベクトル場 もしくは 渦なし場 などと呼びます．スカラーポテンシャル場は， rotgrad=0 によって自動的に層状になります．また，層状ベクトル場の概念は管状ベクトル場と一緒に対概念としてよく使われますので，両方同時に勉強すると良いと思います．次の定理が非常に重要です．

theorem

単連結領域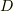で定義されるベクトル場 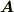$\bm{A}$ がスカラーポテンシャル場であるための必要十分条件は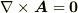， $\nabla \times \bm{A} = \bm{0}$ となることです．

つまり，スカラーポテンシャル場と層状ベクトル場もしくは渦なし場は，同義だと考えても良いということですね．この定理は，電磁気や流体力学といった応用分野でポテンシャル関数を考える際にも必須の定理ですので，よく身に付けてください．

proof

必要条件は 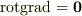${\rm rotgrad}=\bm{0}$ より明らかです．（ rotgrad=0, divrot=0 を参照ください．）十分条件を示します．領域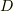内に閉曲線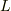を取り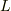，の囲む領域を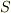とします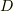．内の至るところ 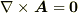$\nabla \times \bm{A}=\bm{0}$ と仮定します．すると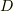，として単連結領域を考えていますのでストークスの定理がなりたち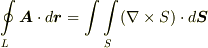， $\ointop \limits_{L} \bm{A} \cdot d\bm{r} = \int \int \limits_{S} (\nabla \times S) \cdot d\bm{S}$ がなりたちます 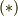(*) ．ここで，任意の線積分 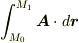$\int_{M_{0}}^{M_{1}} \bm{A} \cdot d\bm{r}$ を考えると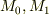， $M_{0},M_{1}$ を通る曲線は幾らでも引けることと式 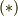(*) より，線積分は経路によらず端点の値だけで決まると言えます．そこで，積分区間の端点 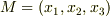$M=(x_{1},x_{2},x_{3})$ だけを変数とする関数 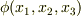$\phi (x_{1},x_{2},x_{3})$ を考え， $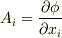A_{i}=\frac{\partial \phi}{\partial x_{i}}$ のように表記することにします．この表記が可能なことは，次のように示せます．まず 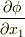$\frac{\partial \phi}{\partial x_{1}}$ という量を考えますが，これは次のように変形できます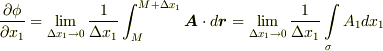． $\frac{\partial \phi}{\partial x_{1}}=\lim \limits _{\Delta x_{1}\rightarrow 0}\frac{1}{\Delta x_{1}}\int_{M}^{M+\Delta x_{1}}\bm{A} \cdot d\bm{r}=\lim \limits_{\Delta x_{1}\rightarrow 0}\frac{1}{\Delta x_{1}}\int \limits_{\sigma} A_{1}dx_{1}$ .ただし， $\sigma$ は $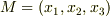M=(x_{1},x_{2},x_{3})$ と $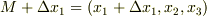M+\Delta x_{1}=(x_{1}+\Delta x_{1},x_{2},x_{3})$ を結ぶ曲線とします．ここで中間値の定理を使うと，次式を満たすような 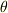$\theta$ が必ず存在するはずです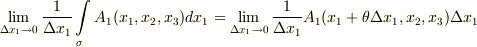． $\lim \limits_{\Delta x_{1}\rightarrow 0}\frac{1}{\Delta x_{1}}\int \limits_{\sigma} A_{1}(x_{1},x_{2},x_{3})dx_{1}=\lim \limits_{\Delta x_{1}\rightarrow 0}\frac{1}{\Delta x_{1}} A_{1}(x_{1}+\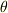theta \Delta x_{1},x_{2},x_{3})\Delta x_{1}$ .ここで $\theta$ は $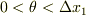0<\theta <\Delta x_{1}$ なので，最後の極限は 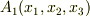$A_{1}(x_{1},x_{2},x_{3})$ に収束し，確かに 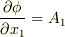$\frac{\partial \phi}{\partial x_{1}}=A_{1}$ が示されます．他の成分も同様ですので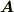， $\bm{A}$ にはスカラーポテンシャル 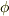$\phi$ が存在することが示されました．■