直交座標系
基底ベクトル 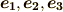 ,もしくは
,もしくは 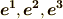 が全て互いに直交するものを 直交座標系 と呼びます.(双対基底の両方が直交基底だと仮定しなくても,どちらかが直交基底ならば,双対基底の定義式により,もう一方も直交基底になることが簡単に示せます.)
が全て互いに直交するものを 直交座標系 と呼びます.(双対基底の両方が直交基底だと仮定しなくても,どちらかが直交基底ならば,双対基底の定義式により,もう一方も直交基底になることが簡単に示せます.)
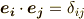
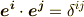
数学や物理学で実際によく使う,デカルト座標系,円筒座標系,球座標系等は全て直交座標系ですから,直交座標系の性質をよく知っておくのは有意義だと思います.
計量テンソルの成分は,その定義により次のように表現されます.

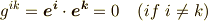
つまり,計量テンソルを行列表記した場合,直交座標系では対角成分以外が全て 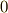 になるということです.
になるということです.
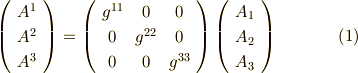

式  に式
に式 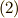 を代入,もしくは式
を代入,もしくは式 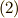 に式
に式 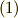 を代入すれば,元に戻るはずですから,二つの行列の積は単位行列になることが要請されます.
を代入すれば,元に戻るはずですから,二つの行列の積は単位行列になることが要請されます.
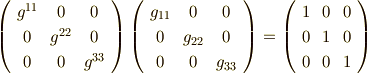
これより,次の関係式が得られます.

また, 計量テンソル の記事で行ったように,微小ベクトルの長さ 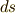 を計量テンソルと基底ベクトルで表現してみると,次式のようになります.
を計量テンソルと基底ベクトルで表現してみると,次式のようになります.
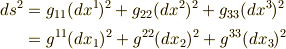
ここで,計量テンソルの対角成分の平方根を特に 計量因子 と呼び, 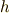 で書きます.
で書きます.
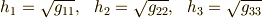

計量因子を用いると, 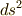 は次のように書きなおせます.
は次のように書きなおせます.
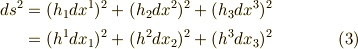
微小長さが,計量テンソルの対角成分と変位成分の二乗だけで表わされています.一般の座標系の場合にあった, 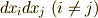 のような項がありません.これはつまり,直交座標系では,長さの計量としてピタゴラスの定理を使っても良いという主張でもあります.
のような項がありません.これはつまり,直交座標系では,長さの計量としてピタゴラスの定理を使っても良いという主張でもあります.
また,直交座標系では共変基底 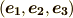 と反変基底
と反変基底  が一致しますので,添字の上下による区別が必要ありません.そこで,今まで気をつけていた添字の区別をやめて,式
が一致しますので,添字の上下による区別が必要ありません.そこで,今まで気をつけていた添字の区別をやめて,式  を次のように書いてしまっても問題ありません.
を次のように書いてしまっても問題ありません.

区別しなくて良いものをわざわざ区別するのは無駄手間ですから,直交座標系の場合に限って添字を全て右下に書くことがあると思いますが,『添字の上下による区別が不要なのは直交座標系の場合に限る』という事情をよく理解しておくことが大事です.
Important
直交座標系には,添字の上下による区別が必要ない.(共変基底と反変基底が一致する.)
| [*] | 例えば,高校で微積分の図形問題を勉強したとき,微小長さは  のように表わしたと思います.しかしよく考えてみると,このようにピタゴラスの定理が成り立つのは のように表わしたと思います.しかしよく考えてみると,このようにピタゴラスの定理が成り立つのは  と と 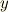 を直角に取っているからなのであって,一般には を直角に取っているからなのであって,一般には 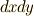 の項も出てくるはずなんですね.これは『物の長さをどう測るか』という問題ですから,幾何学をやる上でとても重要です.例えば,リーマン幾何と呼ばれる曲面上の幾何学では,長さの定義に の項も出てくるはずなんですね.これは『物の長さをどう測るか』という問題ですから,幾何学をやる上でとても重要です.例えば,リーマン幾何と呼ばれる曲面上の幾何学では,長さの定義に 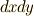 のような長さの対角成分も出てきます. のような長さの対角成分も出てきます. |
計量因子は,直交座標系から直交座標系への座標変換をバリバリと行うようになったときにとても重要になります.座標変換で一番面倒なのは,微分計算の変換ですが,計量因子を使って微分演算子を変換する方法は ベクトル演算子の座標変換 で紹介します.なかなか,実際に手を動かしてみないと計量因子の意味が分かりにくいと思うのですが,微分演算子の座標変換を勉強するまでは,あまり計量因子の活躍の場も無いと思います.まだベクトルの微積分を勉強していない人は『そのうちそんな話題もあるのか』という程度に ,記憶に留めておいて下さい.