多価関数のポテンシャル
積分領域 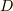 が単連結ではない場合,
が単連結ではない場合, 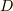 内には少なくとも一本『曲面の境界にはならない閉曲線』を引くことが出来ます.例えば,
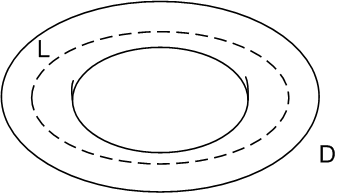
内には少なくとも一本『曲面の境界にはならない閉曲線』を引くことが出来ます.例えば, 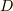 をトーラス(ドーナツ型)だとすると,次図の点線
をトーラス(ドーナツ型)だとすると,次図の点線 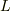 によって囲まれる曲面はありません.
によって囲まれる曲面はありません.
いま,単連結ではない領域 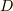 で定義される渦なし場
で定義される渦なし場 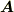 を考えてみましょう.
を考えてみましょう.

渦なし場とスカラーポテンシャルに関して スカラー場と層状ベクトル場 で示した定理の証明では,単連結領域ではストークスの定理が使えるので 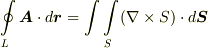 が成り立ち,渦なし場では
が成り立ち,渦なし場では 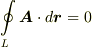 となる事が大きなポイントとなっていました.裏を返せば,多重連結な領域ではストークスの定理がなりたたず,一般に渦なしだからと言って
となる事が大きなポイントとなっていました.裏を返せば,多重連結な領域ではストークスの定理がなりたたず,一般に渦なしだからと言って 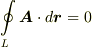 とは言えないということです.このため, 線積分も経路によることになります .
とは言えないということです.このため, 線積分も経路によることになります .
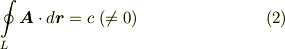
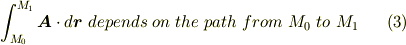
この場合,一価関数のポテンシャル関数から流れ場を与えることは不可能です.線積分が経路によるため,単連結の場合のように,単純に 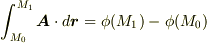 とは出来ないからです.例えば,次図のような状況で線積分
とは出来ないからです.例えば,次図のような状況で線積分 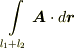 を考えてみましょう.
を考えてみましょう.
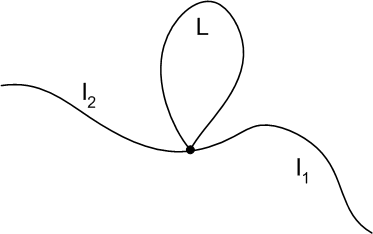
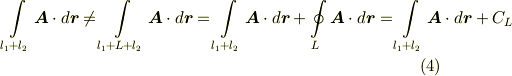
周回積分が 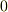 でないことより,経路によって積分値が異なることが分かると思います.このような流れ場に対しては,次式を満たす多価関数のポテンシャルを定義することが出来ます.
でないことより,経路によって積分値が異なることが分かると思います.このような流れ場に対しては,次式を満たす多価関数のポテンシャルを定義することが出来ます.

単連結領域のポテンシャル関数が 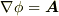 と微分形で与えられたのに比べ,式
と微分形で与えられたのに比べ,式 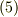 の方は積分で定義されており,もっと緩い条件式であることを確認して下さい.
の方は積分で定義されており,もっと緩い条件式であることを確認して下さい.
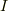 は,ビオ=サヴァールの法則によって,次式で与えられる磁場を作ります.(電磁気学より流体力学の方が好きな人は,これを渦ベクトルと誘起速度場と考えても内容的には同じです.)
は,ビオ=サヴァールの法則によって,次式で与えられる磁場を作ります.(電磁気学より流体力学の方が好きな人は,これを渦ベクトルと誘起速度場と考えても内容的には同じです.)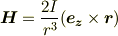
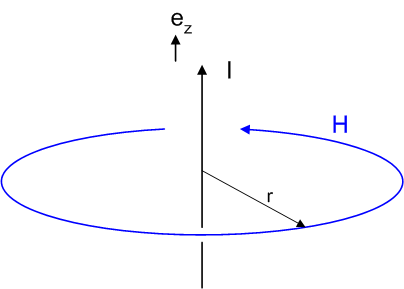
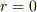 となる
となる  軸を除いて空間全体で定義できます.
軸を除いて空間全体で定義できます. 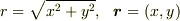 です.)
です.)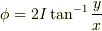 によって,この磁場が表現できることを確認してみてください.(ヒント:
によって,この磁場が表現できることを確認してみてください.(ヒント: 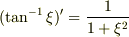 を使いましょう.)
を使いましょう.) の円
の円 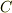 に沿って,周回積分
に沿って,周回積分 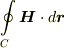 を計算してみて下さい.そして,領域が単連結ではないので,周回積分が
を計算してみて下さい.そして,領域が単連結ではないので,周回積分が