計量テンソル
ベクトル 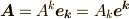 の両辺に,
の両辺に, 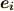 と
と 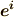 を乗じることで次式を得ます.
を乗じることで次式を得ます.
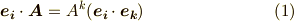
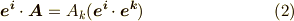
ここまでは単に両辺に内積を取ってみただけで,だからどうってことはありません.今後のために,基底同士の内積は次のような記号で表わすことにしておきましょう.
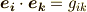
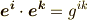
また,補足ですが,双対基底の内積はクロネッカーのデルタになりますから, 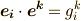 は
は 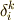 と書いた方が意味は明快ですが,統一性の観点から
と書いた方が意味は明快ですが,統一性の観点から 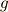 を使うこともあります.ご了承ください.
を使うこともあります.ご了承ください.
さて,式 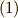 の左辺の
の左辺の 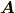 には
には  を,式
を,式 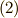 の左辺の
の左辺の 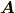 には
には 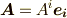 を代入し,
を代入し, 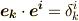 に気をつけると,
に気をつけると, 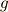 を使って次式を得ます.
を使って次式を得ます.


これはベクトルの共変成分と反変成分の,変換の式になっています.( ベクトル成分の座標変換 を参照して下さい.)添字の 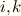 はそれぞれ
はそれぞれ 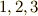 を表わしますから,変換の係数は
を表わしますから,変換の係数は 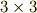 で,
で, 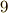 種類あることが分かります.(ただし,内積は順序によりませんので,
種類あることが分かります.(ただし,内積は順序によりませんので, 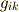 と
と 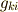 など,添字の順序が逆のものは同じ値になります.本質的に異なるのは
など,添字の順序が逆のものは同じ値になります.本質的に異なるのは 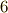 種類です.) 見やすいように,変換係数を次のように行列で表わしておきましょう.添字は
種類です.) 見やすいように,変換係数を次のように行列で表わしておきましょう.添字は 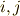 としておきます.
としておきます.
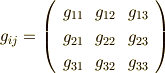
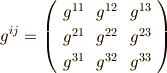
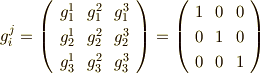
変換係数の意味
共変成分と反変成分の相互の変換を橋渡しする変換係数として, 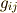 や
や 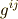 が出てきましたが,これらには図形的にきっちりとした意味があります.このセクションでは,それを見ていきます.
が出てきましたが,これらには図形的にきっちりとした意味があります.このセクションでは,それを見ていきます.
いま,ベクトル  の長さが微小に変化したとします.その微小変化を,微小ベクトル
の長さが微小に変化したとします.その微小変化を,微小ベクトル 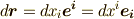 で表わしましょう.
で表わしましょう. 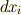 や
や 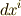 は,各座標系におけるこの微小ベクトルの成分です.ベクトルの長さが少し変わったといっても,観測する座標系によって見え方は違うのですから,
は,各座標系におけるこの微小ベクトルの成分です.ベクトルの長さが少し変わったといっても,観測する座標系によって見え方は違うのですから, 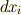 や
や 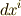 も当然
も当然 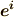 や
や 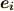 の取り方に依存する量になります.
の取り方に依存する量になります.
微小ベクトルの長さ 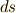 は次式のように内積で定義されます.( 内積空間 参照.)
は次式のように内積で定義されます.( 内積空間 参照.)
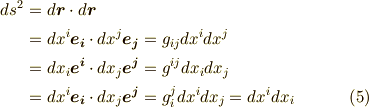
この表式の二行目,三行目,四行目はそれぞれ 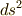 を意味していますが,座標系の取り方が違っています.当然,ベクトル
を意味していますが,座標系の取り方が違っています.当然,ベクトル  の微小な変化
の微小な変化  に対し,異なる座標系では異なる変化分が観測されます.例えば,
に対し,異なる座標系では異なる変化分が観測されます.例えば, 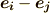 座標系では,
座標系では,  の変化があったように見えるし,
の変化があったように見えるし, 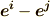 座標系では,
座標系では,  の変化があったように見えるわけです.式
の変化があったように見えるわけです.式  の右辺が意味しているのは,これらの座標系で,各座標軸に沿った変化分の単純な積,
の右辺が意味しているのは,これらの座標系で,各座標軸に沿った変化分の単純な積, 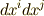 や
や 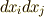 と,本当の変化分の二乗
と,本当の変化分の二乗 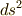 の 比 が
の 比 が 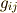 や
や 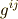 だということです.
だということです.
このように, 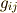 や
や 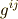 は図形の計量に関係する係数でしたので, 計量テンソル と呼びます.面白いですね.もう一度,式
は図形の計量に関係する係数でしたので, 計量テンソル と呼びます.面白いですね.もう一度,式 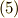 をじっくり眺めてみて下さい.
をじっくり眺めてみて下さい.
| [*] | テンソルの概念はまだ勉強していませんが,計量テンソルは二階のテンソルという量になります.また,直交座標系の場合,計量テンソルの成分の平方根を計量因子と呼びます.テンソルを勉強したあとに,この辺りをもう一度復習してみてください.計量因子は次の 直交座標系 で定義します. ベクトル演算子の座標変換 の記事では,定義はもっと天下り的ですが,計量因子の応用を紹介しています.時間があれば参考にしてみて下さい. |
| [†] | 計量テンソルの意味は具体例を考えるともっと分かりやすいと思います.例えば,二次元デカルト座標 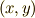 から極座標 から極座標 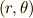 に座標変換すると,微小面積は に座標変換すると,微小面積は 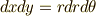 の関係で結ばれます.これは解析学で習ったと思いますが, 右辺に出てきた の関係で結ばれます.これは解析学で習ったと思いますが, 右辺に出てきた  はヤコビアンです.この はヤコビアンです.この  がこの場合の計量テンソルの成分 がこの場合の計量テンソルの成分 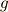 になります.左辺の になります.左辺の 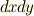 は長さの二乗の次元ですが,右辺の は長さの二乗の次元ですが,右辺の 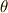 は角度ですので無次元で,計量テンソルの成分 は角度ですので無次元で,計量テンソルの成分  と と 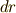 が長さの次元を持っているので辻褄が合うようになっています.このように一般に計量テンソルの成分には長さの次元が入ることがあります.さらに詳しくは 計量テンソルとヤコビアン を参照して下さい. が長さの次元を持っているので辻褄が合うようになっています.このように一般に計量テンソルの成分には長さの次元が入ることがあります.さらに詳しくは 計量テンソルとヤコビアン を参照して下さい. |
さらにもう一歩
計量テンソルとして,基底ベクトルに応じて 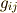 と
と 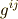 という,添字が上につくものと添字が下につくものが出てきました.このセクションでは,計量テンソルの成分が互いにどのような関係で結ばれているのかを考えてみます.
という,添字が上につくものと添字が下につくものが出てきました.このセクションでは,計量テンソルの成分が互いにどのような関係で結ばれているのかを考えてみます.
ベクトル成分の変換式を,行列の形でもう一度考えて見ましょう.( ベクトル成分の座標変換 参照.)
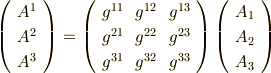
線形代数の知識を少し使うと, 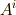 を次のように表わせることが分かります.
を次のように表わせることが分かります.

ただし,式中 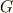 は行列
は行列 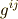 の行列式,
の行列式, 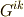 は行列
は行列 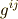 の
の 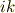 成分の余因子を意味するものとしています.(行列式や余因子について,ここでは詳しく説明できませんので,よく分からない人は自分で線形代数の教科書などを参考にして下さい m(_ _)m.例を書いておきます↓)
成分の余因子を意味するものとしています.(行列式や余因子について,ここでは詳しく説明できませんので,よく分からない人は自分で線形代数の教科書などを参考にして下さい m(_ _)m.例を書いておきます↓)

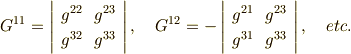
一方,先ほど式 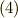 で
で 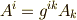 という関係がありましたから,式
という関係がありましたから,式 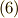 と比較して次式を得ます.
と比較して次式を得ます.

まったく同様にして,共変ベクトルの計量テンソルの成分も次のように表わせることが分かります.

ただし, 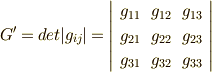 としました.
としました.
ところで, 双対基底 の記事で得た 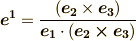 等の公式を使えば,計量テンソルの成分を次のように表現することもできます.式中,
等の公式を使えば,計量テンソルの成分を次のように表現することもできます.式中, 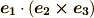 等を
等を 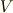 と置いていますが,これは
と置いていますが,これは 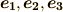 によって張られる平行六面体の体積になります.( 三重積 を参照してください.)また,
によって張られる平行六面体の体積になります.( 三重積 を参照してください.)また, 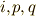 と
と 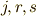 はそれぞれ巡回的な添字だとします.
はそれぞれ巡回的な添字だとします.
![g^{ij}&=\bm{e^{i}} \cdot \bm{e^{j}} \\&=\frac{ (\bm{e_{p}}\times \bm{e_{q}}) }{\bm{e_{i}} \cdot (\bm{e_{p} \times \bm{e_{q}}})} \cdot \frac{ (\bm{e_{r}}\times \bm{e_{s}}) }{\bm{e_{j}} \cdot (\bm{e_{r} \times \bm{e_{s}}})} \\ & = \frac{1}{V^{2}}(\bm{e_{p}}\times \bm{e_{q}}) \cdot (\bm{e_{r}}\times \bm{e_{s}}) \\ & = \frac{1}{V^{2}}((\bm{e_{p}}\times \bm{e_{q}}) \times \bm{e_{r}} )\cdot \bm{e_{s}} \\ & = \frac{1}{V^{2}}[\bm{e_{q}}(\bm{e_{p}}\cdot \bm{e_{r}}) - \bm{e_{p}}(\bm{e_{q}}\cdot \bm{e_{r}})]\cdot \bm{e_{s}} \\ & = \frac{1}{V^{2}}[(\bm{e_{p}} \cdot \bm{e_{r}})(\bm{e_{q}} \cdot \bm{e_{s}}) - (\bm{e_{p}} \cdot \bm{e_{s}})(\bm{e_{q}} \cdot \bm{e_{r}}) ] \\ & = \frac{1}{V^{2}}\left| \begin{array}{cc}\bm{e_{p}} \cdot \bm{e_{r}} & \bm{e_{p}} \cdot \bm{e_{s}} \\\bm{e_{q}} \cdot \bm{e_{r}} & \bm{e_{q}} \cdot \bm{e_{s}} \\\end{array}\right| \\ & = \frac{1}{V^{2}}\left| \begin{array}{cc}g_{pr} & g_{ps} \\g_{qr} & g_{qs} \\\end{array}\right| \tag{9}](./8b70b62956835d8cc6f3b6ca52f334a3.png)
色々,細かいテクニックを使って式変形をしましたが,最後はなんだか不思議に簡単な表式に至りました.さきほど,式  として
として  という式を得ていましたが,これを式
という式を得ていましたが,これを式 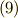 と比較することで次式を得ます.
と比較することで次式を得ます.

平方根を展開すると 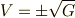 となりますが,この符号は
となりますが,この符号は 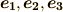 が右手系ならば正,左手系ならば負になるように決められます.( 三重積 を参照してください.)
が右手系ならば正,左手系ならば負になるように決められます.( 三重積 を参照してください.) 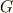 の図形的意味は,これで少し分かりました. det|G|は基底の張る平行六面体の体積の二乗になっています .
の図形的意味は,これで少し分かりました. det|G|は基底の張る平行六面体の体積の二乗になっています .
同様にして,共変ベクトルの計量テンソルの成分に対しても次式が導けます.
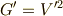
計量テンソルの表現行列には,意外と分かりやすい図形的意味があるようです.また,次の関係に注意してみましょう.
![1&=\bm{e_{1}}\cdot \bm{e^{1}} \\&=\frac{\bm{e^{2}} \times \bm{e^{3}}}{V'}\frac{\bm{e_{2}} \times \bm{e_{3}}}{V} \\&= \frac{1}{VV'} (\bm{e^{2}} \times \bm{e^{3}})\cdot (\bm{e_{2}} \times \bm{e_{3}}) \\ &= \frac{1}{VV'} [(\bm{e^{2}} \cdot \bm{e_{2}})(\bm{e^{3}} \cdot\bm{e_{3}} )-(\bm{e^{3}} \cdot \bm{e_{2}})(\bm{e^{2}}\cdot \bm{e_{3}})] \\ &= \frac{1}{VV'}](./5fef47f6bb943ecc595c9f5c28e7a56b.png)
これより, 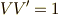 の関係は座標系に関わらず常になりたつことが分かりました.式
の関係は座標系に関わらず常になりたつことが分かりました.式 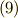 より
より 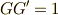 も言えます.またしても,双対基底に関する美しい関係式が得られました!
も言えます.またしても,双対基底に関する美しい関係式が得られました!