スカラー関数の線積分
この記事では,線積分という積分を勉強します.次の記事以降ではベクトルの線積分を考えますが,まず線積分という計算になれるためにスカラーを線積分するところから始めようと思います.解析学的な立場で厳密に考えることはしません.あくまで,直観的なイメージ重視でいきます.
線積分
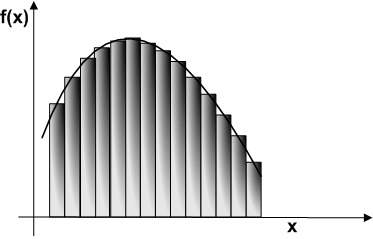
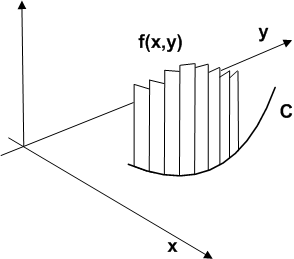
高校で最初に積分を習ったとき,次図のようなイメージを使った人が多いかと思います.
変数  の各点で定義される関数
の各点で定義される関数 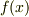 の値に
の値に 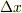 を掛け,この微小面積を
を掛け,この微小面積を  の全範囲に渡って足し合わせた量を考えます.図では,短冊状の長方形領域が幾つか描かれていますが,この幅を極限まで狭くし,かわりに無限に多くの短冊状領域を考えた極値的が
の全範囲に渡って足し合わせた量を考えます.図では,短冊状の長方形領域が幾つか描かれていますが,この幅を極限まで狭くし,かわりに無限に多くの短冊状領域を考えた極値的が 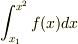 という量になります.動的なイメージとしては,この積分は変数
という量になります.動的なイメージとしては,この積分は変数  が
が  軸という 直線の上 を
軸という 直線の上 を 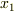 から
から 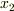 まで動くとき,時々刻々
まで動くとき,時々刻々 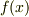 の値を足していった総和が積分だと考えても良いでしょう.ここまでは,高校数学の復習です.
の値を足していった総和が積分だと考えても良いでしょう.ここまでは,高校数学の復習です.
さて,二変数関数 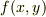 を積分するときも要点は全く同じで,各点
を積分するときも要点は全く同じで,各点 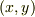 で定義される関数
で定義される関数 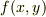 の値を全範囲に渡って足し合わせることを考えますが,『
の値を全範囲に渡って足し合わせることを考えますが,『  と
と 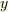 がどう動くか』という点について,もう少しよく考えないといけません.一変数の場合は変数の動き方は一次元的で, 積分区間 と呼べるものでしたが,二変数の場合,変数
がどう動くか』という点について,もう少しよく考えないといけません.一変数の場合は変数の動き方は一次元的で, 積分区間 と呼べるものでしたが,二変数の場合,変数 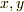 が
が 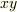 平面上でどのような領域を動くのかを考えないといけません.積分領域は
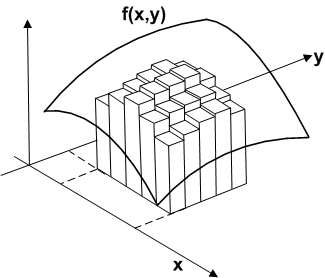
平面上でどのような領域を動くのかを考えないといけません.積分領域は 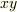 平面上で何か平面図形になるでしょう.例えば,次図は積分領域が長方形の場合のイメージ図です.各点
平面上で何か平面図形になるでしょう.例えば,次図は積分領域が長方形の場合のイメージ図です.各点 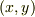 で定義される関数
で定義される関数 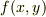 の値に
の値に 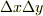 を掛けた四角柱の 体積 を,全体に渡って足し合わせるイメージです.|064cb6fda6922748c28e702d89c98984| ,
を掛けた四角柱の 体積 を,全体に渡って足し合わせるイメージです.|064cb6fda6922748c28e702d89c98984| , 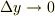 の極限を取り,その代わりに無限に多くの四角柱を考えることにすれば,積分
の極限を取り,その代わりに無限に多くの四角柱を考えることにすれば,積分 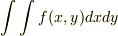 を得ます.
を得ます.
今のような話は,重積分を勉強したことがある人は知っていると思います.また,積分領域が曲線である積分を 線積分 と呼びます.線積分は,最初の短冊型領域の面積を足していくイメージで考えれば良いですが,短冊型領域を考えるのは直線上ではなく曲線上になります.
曲線を 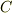 ,関数を
,関数を 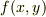 として,線積分は次のように表わされます.
として,線積分は次のように表わされます. 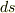 を曲線の微小な弧の長さとすると,
を曲線の微小な弧の長さとすると, 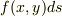 が微小短冊型領域の面積になります.(
が微小短冊型領域の面積になります.(  については 空間曲線と接線の方程式 を参照してください.)
については 空間曲線と接線の方程式 を参照してください.)

もし, 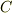 が空間曲線なら三変数で次のようになります.
が空間曲線なら三変数で次のようになります.

| [*] | 四次元以上の線積分を考えることはあまりありませんが,同じように変数を増やすことで何次元にでも拡張できます. |
弧長パラメーター 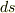 に関して,デカルト座標系なら
に関して,デカルト座標系なら 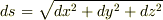 と書けて,ベクトル表示で
と書けて,ベクトル表示で 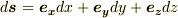 のように表わすことも可能です.普通は
のように表わすことも可能です.普通は 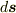 とか書かずに
とか書かずに 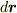 と書きます.線積分をベクトル表示にすれば,以下のようになります.
と書きます.線積分をベクトル表示にすれば,以下のようになります.
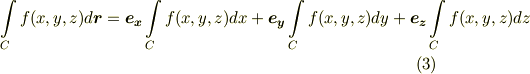
線積分の計算
実際に線積分を計算するときには,積分経路となる曲線の方程式が必要です.例えば,曲線が 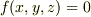 の形で与えられるとき,この曲線に沿って
の形で与えられるとき,この曲線に沿って 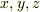 がどう動くのかを記述するのはかなり面倒です(方程式
がどう動くのかを記述するのはかなり面倒です(方程式 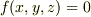 を解くのと同じ手間がかかります.).もし,曲線がパラメーター表示できるなら,『曲線上を点
を解くのと同じ手間がかかります.).もし,曲線がパラメーター表示できるなら,『曲線上を点 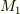 から
から 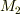 まで動く』という条件を『パラメーター
まで動く』という条件を『パラメーター 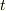 が
が 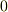 から
から 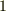 まで動く』のように言い換えることができ,実質的に一変数の積分にまで問題を簡単化することが出来ます.パラメーター表示がお薦めです.
まで動く』のように言い換えることができ,実質的に一変数の積分にまで問題を簡単化することが出来ます.パラメーター表示がお薦めです.
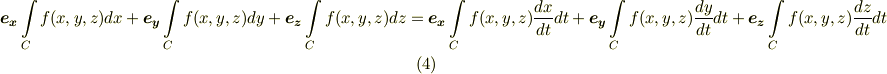
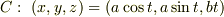 に沿って,関数
に沿って,関数 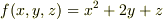 の線積分
の線積分 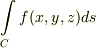 を求めて下さい.
を求めて下さい.  まで動くものとします.
まで動くものとします.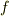 を
を 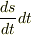 を求めましょう.
を求めましょう. 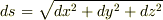 を使ってください.
を使ってください.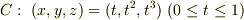 に沿って,関数
に沿って,関数 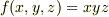 の線積分
の線積分 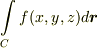 を求めて下さい.
を求めて下さい.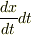 ,
, 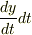 ,
, 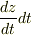 を求めてください.
を求めてください.