色々な線積分
ここまでに,スカラー関数の線積分と,ベクトル場の曲線に沿った線積分を考えました.

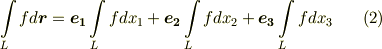
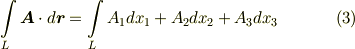
ベクトル場の線積分には,他の形もあります.式 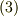 は,積分の中身が内積の形になってものでしたが,線積分というのは,曲線に沿った積分領域を考えるということであって,被積分関数には色々あって良いのです.三次元ベクトルで基本的な演算には,内積の他にスカラー積と外積がありましたから,以下のような線積分を考えることもできます.
は,積分の中身が内積の形になってものでしたが,線積分というのは,曲線に沿った積分領域を考えるということであって,被積分関数には色々あって良いのです.三次元ベクトルで基本的な演算には,内積の他にスカラー積と外積がありましたから,以下のような線積分を考えることもできます.
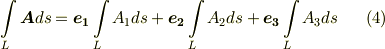
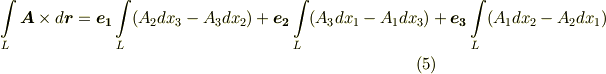
ポテンシャルという概念との相性の良さからか,物理の問題によく出て来るベクトル場の線積分の多くは式  の内積形ですが,この際,線積分には他にも色々あることをまとめて覚えてしまいましょう.一度に並べて眺めてみると,数学的には見通しが良くなると思います.
の内積形ですが,この際,線積分には他にも色々あることをまとめて覚えてしまいましょう.一度に並べて眺めてみると,数学的には見通しが良くなると思います.
| [*] | 上記の  つで,スカラーとベクトルの組み合わせとして『スカラー つで,スカラーとベクトルの組み合わせとして『スカラー  スカラー』『スカラー スカラー』『スカラー  ベクトル』『ベクトル ベクトル』『ベクトル  ベクトル』『ベクトル ベクトル』『ベクトル  スカラー』『ベクトル スカラー』『ベクトル  ベクトル』を網羅していることを確認してください.『ベクトル ベクトル』を網羅していることを確認してください.『ベクトル  ベクトル』なんていうのを知っている人もいるかも知れませんね.実際,そんな量の線積分を考えることも出来ます.いろいろあります. ベクトル』なんていうのを知っている人もいるかも知れませんね.実際,そんな量の線積分を考えることも出来ます.いろいろあります. |
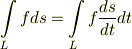
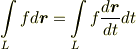
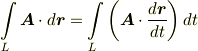
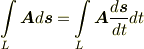
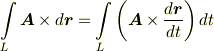
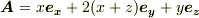 を,始点を
を,始点を 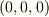 ,終点を
,終点を 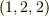 とする線分に沿って線積分します.次の値を計算して下さい.
とする線分に沿って線積分します.次の値を計算して下さい.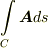
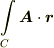
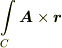
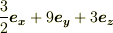 (2)
(2) 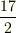 (3)
(3) 